Teorema de Tales

Dicho de otro modo, si cortamos un triángulo dibujando una recta paralela a uno de sus lados, obtendremos un triángulo semejante al previamente existente.

En este punto, cabe señalar que dos triángulos son semejantes cuando sus ángulos correspondientes son congruentes (miden lo mismo) y sus lados homólogos son proporcionales entre sí.

Para entenderlo mejor, observemos la siguiente figura:

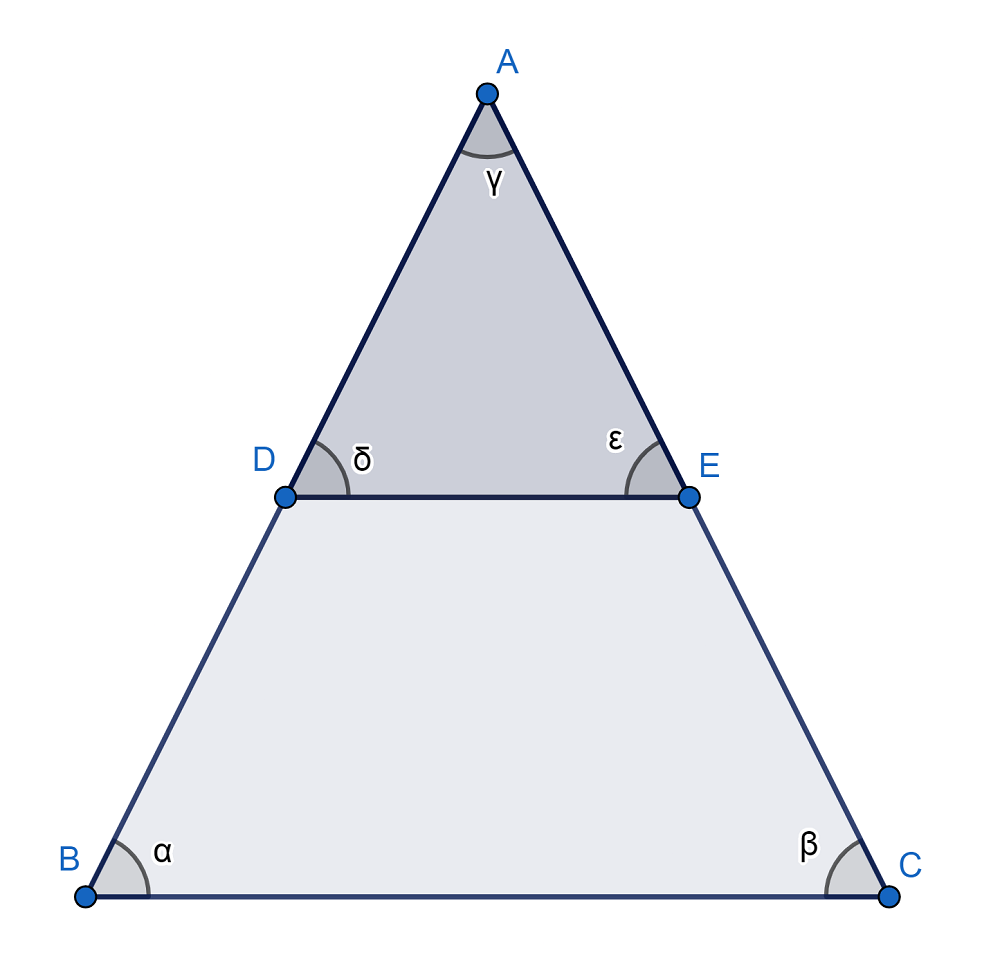
Por el teorema de Tales se puede concluir que α=δ y β=ε

Además, como mencionamos previamente, los lados son proporcionales, por lo que se cumple que:

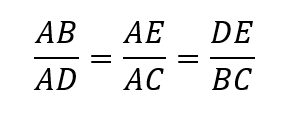
Una anécdota relatada por el historiador Plutarco cuenta que Tales de Mileto, en uno de sus viajes, hizo uso de este teorema para conocer la altura de las pirámides de Guiza (las de Keops, Kefrén y Micerino) en Egipto. Así, decidió poner una vara en vertical contra el suelo, esperando a que la longitud del objeto sea igual a la sombra que proyectaba. En ese momento, la sombra de la pirámide también sería igual a la altura de esta. En este caso, los triángulos semejantes son:

• El que tiene como dos de sus lados la vara y su sombra.
• El triángulo que tiene como uno de sus lados la altura de la pirámide y, como otro lado, la sombra de esta.

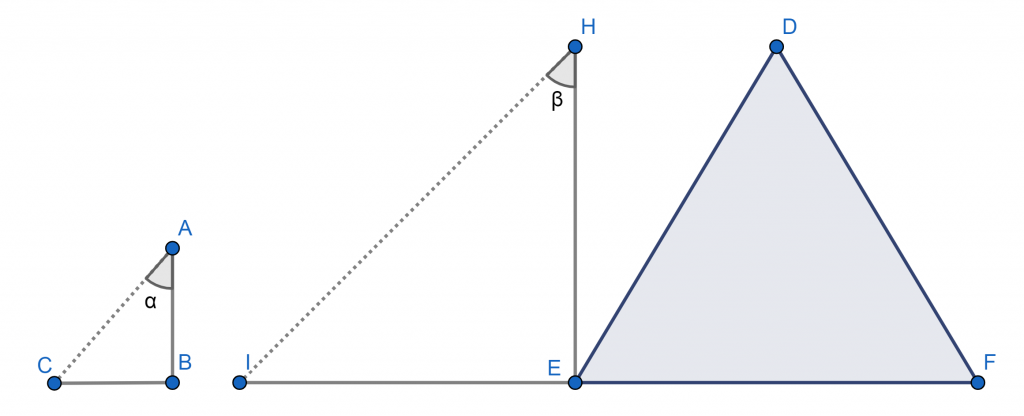
Para entenderlo mejor, imaginemos en la figura de arriba que la pirámide es aquella formada por los vértices D, E y F, su altura es el segmento HE y su sombra, IE. En tanto, la vara es el segmento AB y su sombra, CB. Por tanto, AB/CB=HE/IE. Esto, tomando en cuenta que los rayos del sol son paralelos (no se cruzan ni en su prolongación), por lo que formarán el mismo ángulo con la vara que con la pirámide (ángulos α y β son iguales).

Para entender mejor el teorema de Tales, observemos la siguiente figura:

Si BC mide 7,3 metros, DE mide 3,6 metros y AB mide 6,2 metros. ¿Cuál es la longitud de AD?

Despejamos en la fórmula mostrada previamente y tenemos que:

7,3/3,6=6,2/AD

2,0278=6,2/AD

AD=3,0575 metros

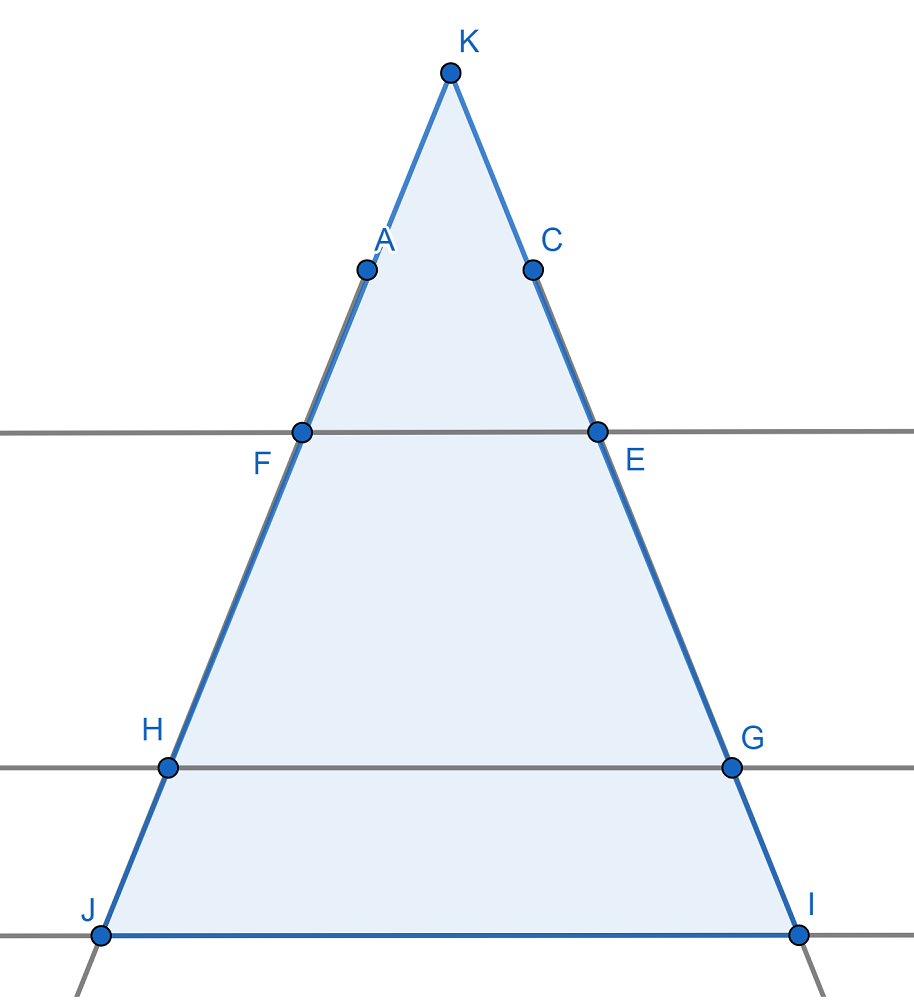
El teorema de Tales puede extenderse al análisis de dos líneas cualquiera que son cortadas por otras líneas paralelas entre sí, como vemos en la siguiente imagen:

Entonces, se cumple que:

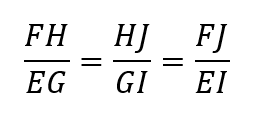
Lo anterior se cumple porque debemos pensar en esas líneas como parte de un triángulo o, viéndolo de otro modo, si extendemos las líneas AB y CD, estas se cruzarán. Mejor lo vemos en la siguiente imagen:

Existe también un segundo teorema de Tales según el cual, si tenemos un triángulo formado por el diámetro de una circunferencia y dos líneas secantes a la misma (cortan la figura en dos puntos), aquel ángulo que está frente al diámetro es recto, es decir, mide 90º.

Cabe recordar que un diámetro es aquel segmento que, pasando por el centro de la circunferencia, uno dos puntos opuestos de dicha figura.

Lo anterior lo podemos observar mejor en la siguiente imagen:

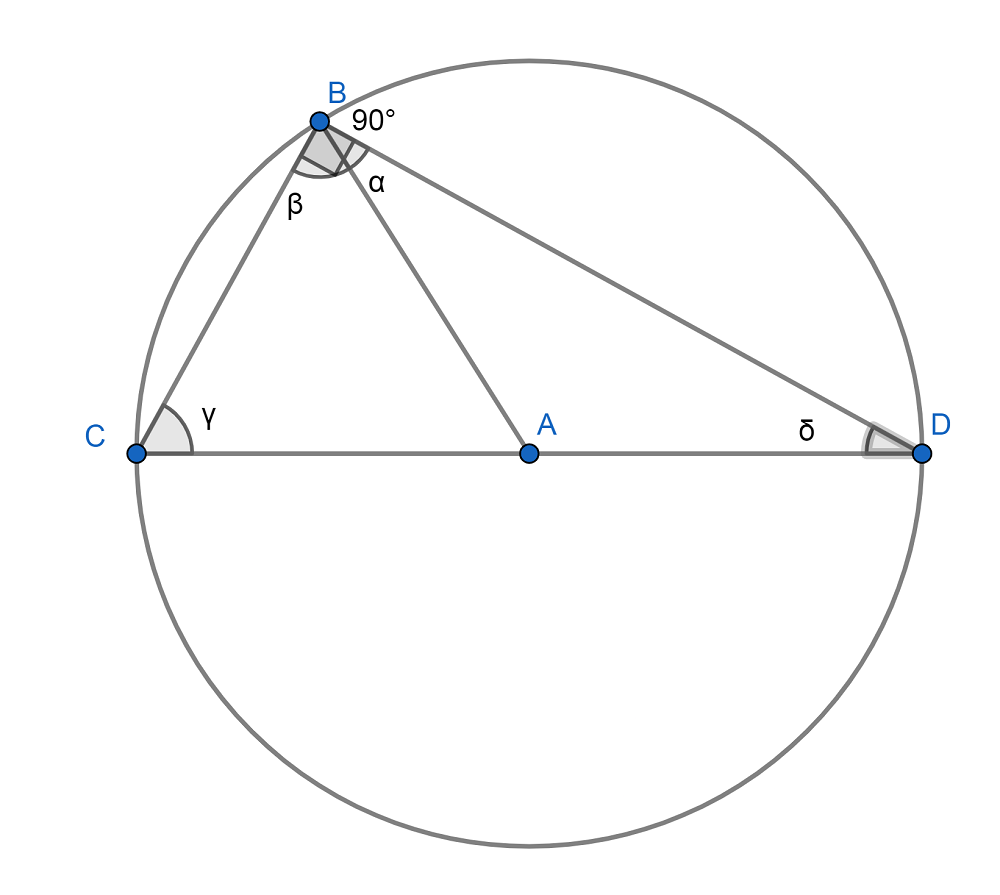
Este teorema lo podemos comprobar tomando en cuenta que AC, AD y AB miden lo mismo y son iguales al radio de la circunferencia (el radio es cualquier segmento que une un punto de la circunferencia con el centro de la figura y es igual a la mitad del diámetro). Entonces, lo triángulos ABC y ABD son isósceles y sus dos lados que son similares están opuestos a ángulos que también miden lo mismo, es decir:

AC=AD=AB= r (radio de la circunferencia)

γ=β y α=δ

Luego, si vemos el triángulo CBD y recordamos que los ángulos internos de un triángulo deben sumar 180º, tenemos que:

γ+β +α+δ=180º

2β+2α=180º

2(α+β)=180º

α+β=90º

Por lo tanto, el triángulo CBD es un triángulo rectángulo.

me interesa seguir sus publicaciones.
Gracias

Excelente