Tasa anual equivalente (TAE)
El acrónimo TAE responde a Tasa Anual Equivalente o Tasa Anual Efectiva. Nos ofrece un valor más cercano a la realidad del coste (en caso de un préstamo) o rendimiento (si se trata de un depósito) del producto financiero contratado.
La TAE nos ofrece un valor más fiel que el que revela la tasa de interés nominal (TIN), ya que incluye en su cálculo, además del tipo de interés nominal, los gastos y comisiones bancarias y el plazo de la operación.
Aunque siempre tendremos que tener en cuenta que estamos comparando. Por ejemplo, la TAE de una hipoteca siempre va a ser más alta que la de un préstamo personal con la misma tasa de interés nominal (TIN), porque la hipoteca suele conllevar más comisiones (comisión de estudio, de apertura…). Ver diferencia entre TIN y TAE.
Por tanto, la TAE nos proporciona un dato más fiel pero no exacto, aunque en su cálculo incluye más premisas que el tipo de interés nominal, no incluye todos los gastos. Por ejemplo, no incluye gastos notariales, impuestos, gastos por transferencia de fondos, gastos por seguros o garantías, etc.
¿Qué nos indica la TAE?
Esto se traduce en que una vez contratado el depósito, sabrás la cantidad que has invertido, la TAE de la operación, el vencimiento y poniendo en común todos estos datos obtendrás un valor que se supone debiera ser el rendimiento de la operación.
Como podrás comprobar cuando te abonen los intereses, estos serán menores que el resultado matemático que habías obtenido. ¿Por qué? Por lo explicado anteriormente, hay gastos que la TAE no incluye. Nada es perfecto y tampoco lo va a ser esto. De ser posible el empleado del banco que vendió el depósito te habría informado del rendimiento exacto de la operación.
Fórmula de la TAE
La fórmula de la TAE es la siguiente:
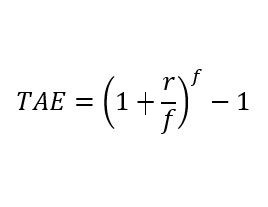
Dónde:
- r: Tipo de interés del préstamo. Es decir, el tipo de interés nominal (TIN)
- f: Se trata de la frecuencia de pagos durante un año. Si se paga una vez al mes, en un año, serán 12 pagos (1 pago cada mes). Si se paga cada trimestre (tres meses), se pagaría 4 veces al año: f = 4. Si se paga de forma anual: f = 1.
A continuación mostramos un ejemplo de cálculo de la TAE.
Ejemplo práctico de la TAE
Ayudémonos de un ejemplo de cálculo de la TAE para comprender mejor la distinción entre tipo de interés nominal y la TAE.
Imaginemos que un banco nos ofrece la posibilidad de contratar un depósito a 12 meses a un tipo de interés del 10%, cuyos intereses se liquidarán al cabo de los 12 meses, al finalizar la operación. DEPÓSITO A
Otro banco, nos pone encima de la mesa un depósito aparentemente muy similar. La única diferencia es que los intereses se liquidan mensualmente sobre el mismo depósito. DEPÓSITO B
En el DEPÓSITO A, el rendimiento es 100€ por cada 1.000€ invertidos. En este caso el tipo de interés nominal coincide con la TAE (10%).
Mientras en el DEPÓSITO B, el rendimiento es de 104,71€ por cada 1.000€ invertidos ¿Cómo puede ser? Muy sencillo, porque recibimos el interés mensualmente, incrementado así el capital sobre el que aplicamos el tipo de interés nominal del 10% para el cálculo de los intereses del mes siguiente (conocido como interés compuesto). Resolviendo, obtenemos una TAE para el DEPÓSITO B de 10,47%, superior al de A. Veamos el paso a paso de cómo llegamos a ese resultado.
Tomando en cuenta la fórmula previamente presentada, r es igual a 10% y f es igual a 12, pues nos referimos a una frecuencia mensual. Entonces:
TAE = (1+(10%/12))^12-1
TAE =(1+(0,1/12)^12)-1
TAE =(1+(0,0083))^12-1
TAE =(1,0083)^12-1
TAE = 1,1047-1=0,1047
TAE =10,47%
El rendimiento de 104,71€ que mencionamos previamente se calculó de la siguiente forma:
1.000*10,47%= 104,71€
Conclusiones sobre la TAE
La TAE nos facilita la tarea de comparar los productos financieros que nos ofrecen los bancos, quienes están obligados por el Banco de España a presentarlo en sus campañas publicitarias.
Eso sí, no nos dejemos cegar por una TAE mayor (si se trata de depósitos o menor en caso de préstamos). Puede darse el caso de que por unas décimas de mejor TAE tengamos que contratar una tarjeta de crédito. Esto puede suponer un gasto de mantenimiento mayor que lo que ganamos por esas décimas de la TAE. Por tanto, es recomendable leer la letra pequeña.
