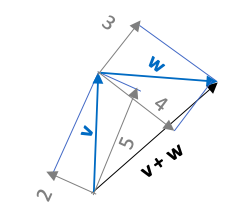
Suma de vectores
La suma de vectores es formar una cadena de vectores donde el vector que engloba a todos los vectores es el vector de la suma.
En otras palabras, la suma de vectores es la unión de vectores a través de juntar la parte delantera de un vector con la parte trasera del otro y cumple con la propiedad conmutativa.
Un vector de dimensión n es una fila que contiene n números reales, se representa a través de un segmento con sentido y dirección y, sirve para representar magnitudes físicas como el volumen, la presión, la energía…
La suma de vectores
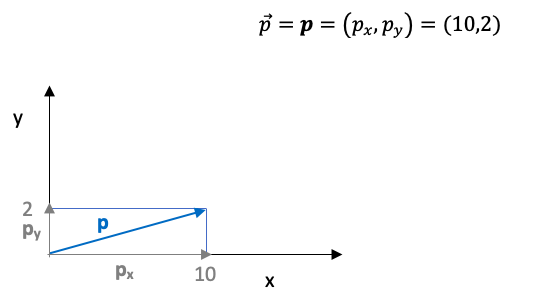
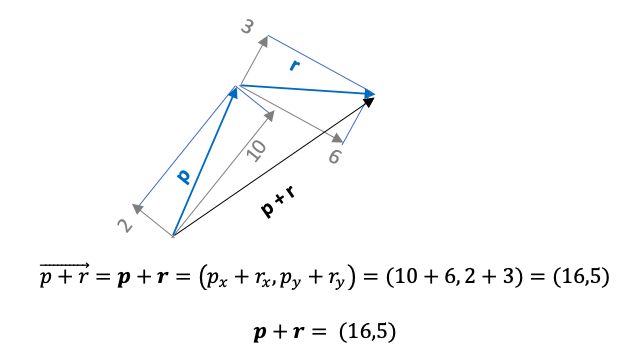
Dados dos vectores p y r, podemos realizar la siguiente operación. Primero dividiremos los vectores en dos vectores para que sea más fácil operar con ellos.
Vector p
Dividimos el vector p en dos vectores:
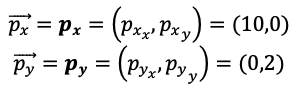
Vector r
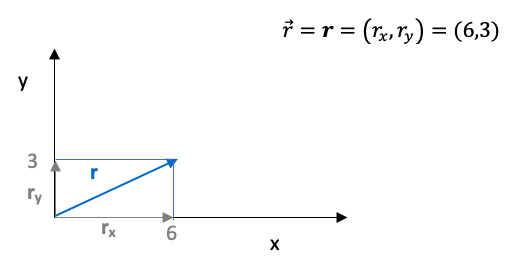
Dividimos el vector r en dos vectores:
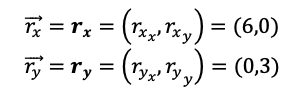
Podemos unir dos vectores juntando la parte trasera de un vector con la parte delantera de otro vector, tal que así:

El resultado de esta unión será la suma del vector p y del vector r, indicada por el vector de color negro p + r. Tal que:
Propiedad conmutativa
La propiedad conmutativa de los vectores aparece cuando podemos expresar la suma de p + r como r + p, es decir, p + r = r + p. No importa el orden en el cual sumemos los vectores r y p.
Aplicación
La suma de vectores la encontramos en la vida cotidiana de las matemáticas y en todas las ciencias que dependen de ellas, ya sean la estadística, física, ingeniería…
Ejemplo
Sumar los siguientes vectores:
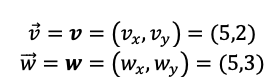
Primero, dividimos cada vector en sus coordenadas de la forma:
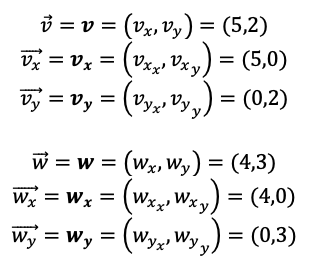
Segundo, sumamos las coordenadas que se correspondan de cada vector:
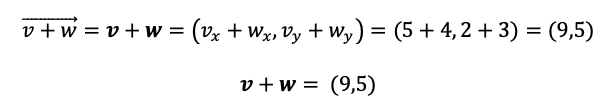
De forma analítica: