Rectas oblicuas

Para entenderlo de otro modo, dos rectas oblicuas se intersecan formando dos ángulos agudos (de menos de 90º) y dos ángulos obtusos (de más de 90º). Todos los cuales suman un ángulo completo (de 360º).

Las rectas oblicuas son un tipo de rectas secantes, es decir, que se cortan en un punto. Asimismo, dos rectas oblicuas no son perpendiculares (que forman cuatro ángulos de 90º), ni pueden ser paralelas (aquellas que no se cruzan en ningún punto).

Cabe recordar que la recta es una secuencia de puntos infinita que va hacia una sola dirección, es decir, no presenta curvas.

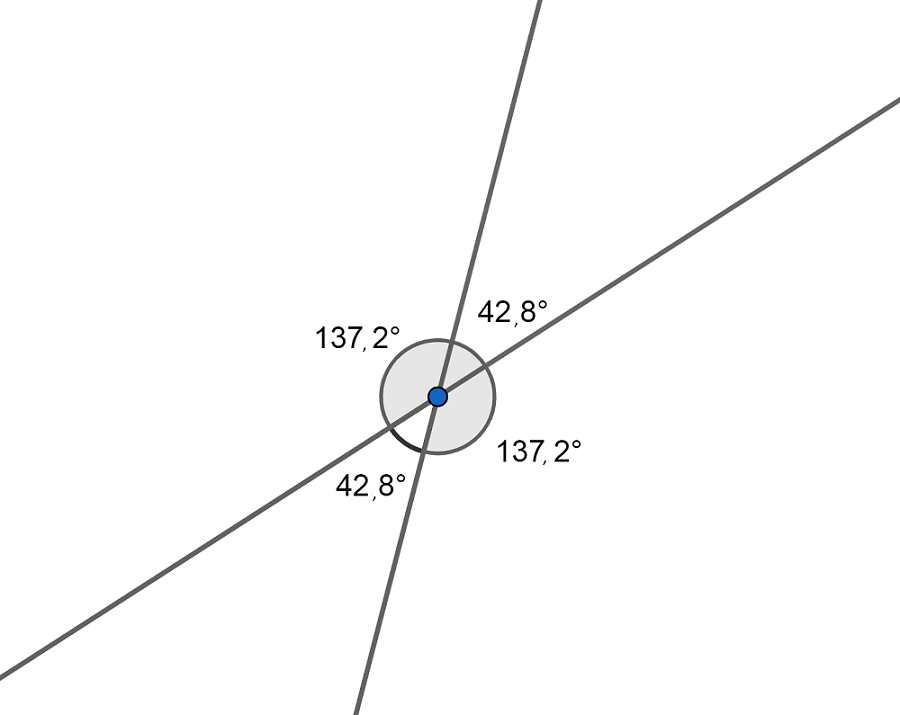
En el ejemplo, podemos ver cómo dos rectas oblicuas forman cuatro ángulos, siendo una propiedad importante que los ángulos agudos, que en el ejemplo son los de que miden 42,8º, son iguales y se encuentran uno al lado opuesto que el otro. Lo mismo sucede con los ángulos obtusos (que en el ejemplo miden 137,2º).

Recordemos además que, desde la geometría analítica, dos rectas son oblicuas cuando su pendiente no es la misma (caso en el cual serían paralelas) y tampoco se cumple que la pendiente de una sea igual al inverso de la pendiente de la otra con el signo invertido (caso en el cual serían perpendiculares).

Debemos apuntar además, que las rectas pueden ser descritas a través de una ecuación como la siguiente:

y=mx+b

Así, en la ecuación y es la coordenada en el eje de las ordenadas (vertical), x es la coordenada en el eje de las abscisas (horizontal), m es la pendiente (inclinación) que forma la recta respecto al eje de las abscisas, y b es el punto en el que la recta corta el eje de las ordenadas.

Veamos un ejemplo para determinar si dos rectas son oblicuas. Supongamos que la recta 1 pasa por el punto A(3,1) y el punto B(-3,4). Asimismo, la recta 2 pasa por el punto C(8,3) y el punto D(-7,-3). ¿Ambas rectas son oblicuas?

Primero, hallamos la pendiente de la recta 1, dividiendo la variación en el eje y entre la variación en el eje X. Esto, cuando pasamos del punto A al punto B. Entonces, en el eje y, pasamos de 1 a 4, por lo que la variación es 3, mientras que en el eje x pasamos de 3 a -3, siendo la variación -6. Entonces, siendo m1 la pendiente de la recta 1, la calculamos:

m1=(4-1)/(-3-3)= 3/(-6)=-0,5

De igual modo, hacemos el mismo procedimiento con la recta 2 para hallar su pendiente (m2), suponiendo que pasamos del punto C al punto D:

m2=(-3-3)/(-7-8)=-6/-15=0,4

Como observamos, las rectas tienen diferentes pendientes y una no es el inverso de la otra con el signo cambiado (esto sucedería si m1 es -0,5 y m2 es 2, por ejemplo). Por tanto, la recta 1 la recta 2 son rectas oblicuas.