Perímetro

El perímetro se refiere entonces a la medida de lo que rodea una figura geométrica, siendo una de sus magnitudes más importantes. Esto, junto al área, que corresponde a lo contenido dentro de la figura.

Calcular el perímetro de un espacio es útil, por ejemplo, en el caso que debamos construir una cerca o muro alrededor de él.

Como mencionamos previamente, para calcular el área de un perímetro, debemos sumar la longitud de cada uno de sus lados, como observamos en la siguiente fórmula, donde n es el número de lados y L es la longitud de cada uno de ellos.

Debemos recordar que el polígono es una figura bidimensional conformada por segmentos consecutivos no colineales, constituyendo un espacio cerrado.

En el caso de un polígono regular, cuyos lados y ángulos interiores tienen todos la misma medida, solo se debe multiplicar la longitud del lado por el número de lados de la figura.

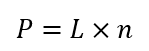
Por ejemplo, en el caso de un cuadrado, que es un polígono regular, si su lado mide 7 metros, su perímetro se calcularía de la siguiente forma:

Para calcular el perímetro de un circunferencia, necesitaremos el radio y/o del diámetro de la misma, siguiendo la siguiente fórmula:

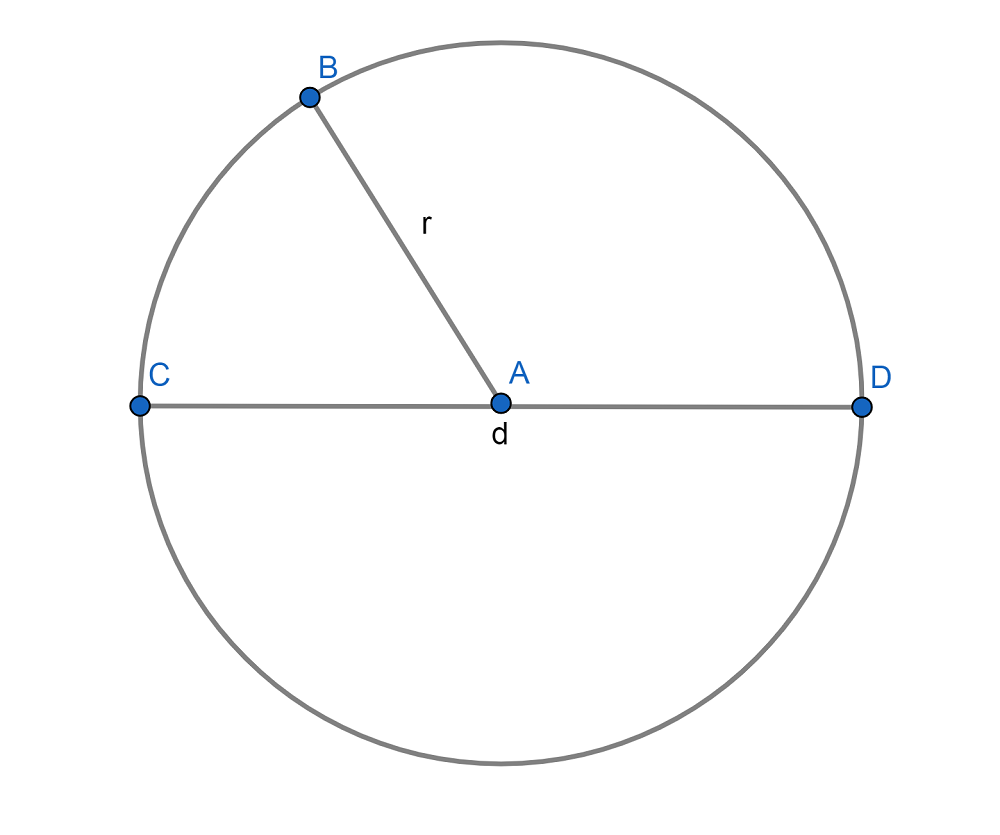
En la ecuación de arriba, r es el radio. Es decir, es la longitud del segmento que une el centro del circulo con cualquiera de los puntos de la circunferencia. Asimismo, d es el diámetro que es la línea que une dos puntos opuestos de la circunferencia y mide el doble del radio. Podemos verlo en la imagen inferior donde el segmento CD es el diámetro y AB es el radio.

Asimismo, para hallar el perímetro de una semicircunferencia, tendríamos que seguir esta otra fórmula:

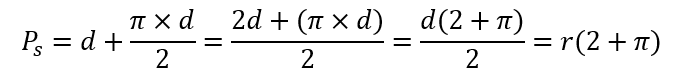
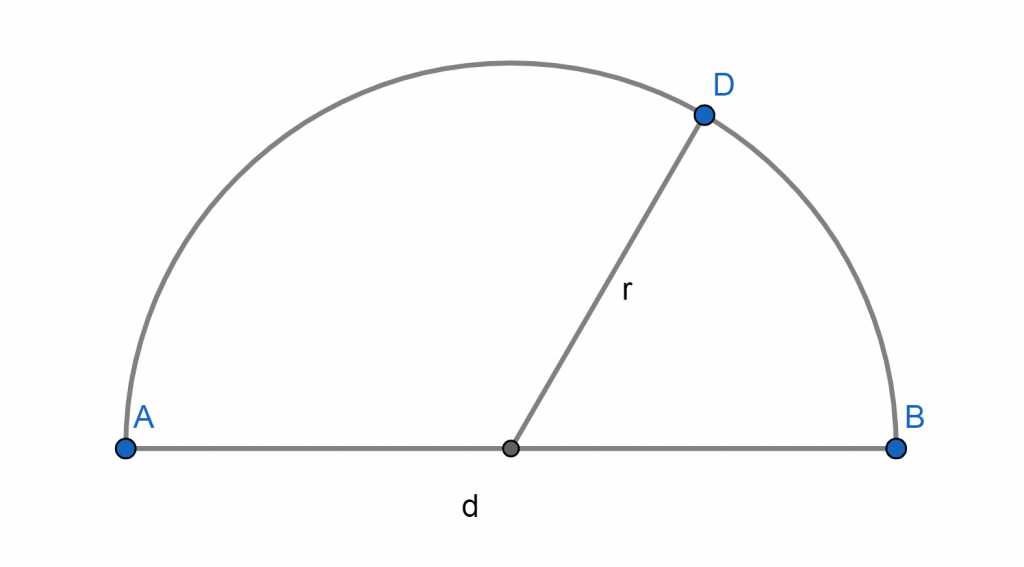
En la ecuación de arriba se puede interpretar que se está sumando el diámetro más el perímetro de la respectiva circunferencia dividido entre dos. Podemos observar esto en la imagen inferior donde el segmento AB es el diámetro.

Entonces, si tenemos una circunferencia con un radio de 10 metros, su perímetro sería:

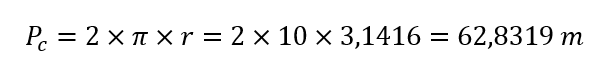
Asimismo, el perímetro de su semicircunferencia sería: