Ángulo interior
Es ángulo interior es aquel arco formado por dos lados de un polígono, de manera que está contenido dentro de la figura.
Es decir, el ángulo interior es aquel arco que se constituye por la intersección de dos lados del polígono, ubicándose dentro del mismo.
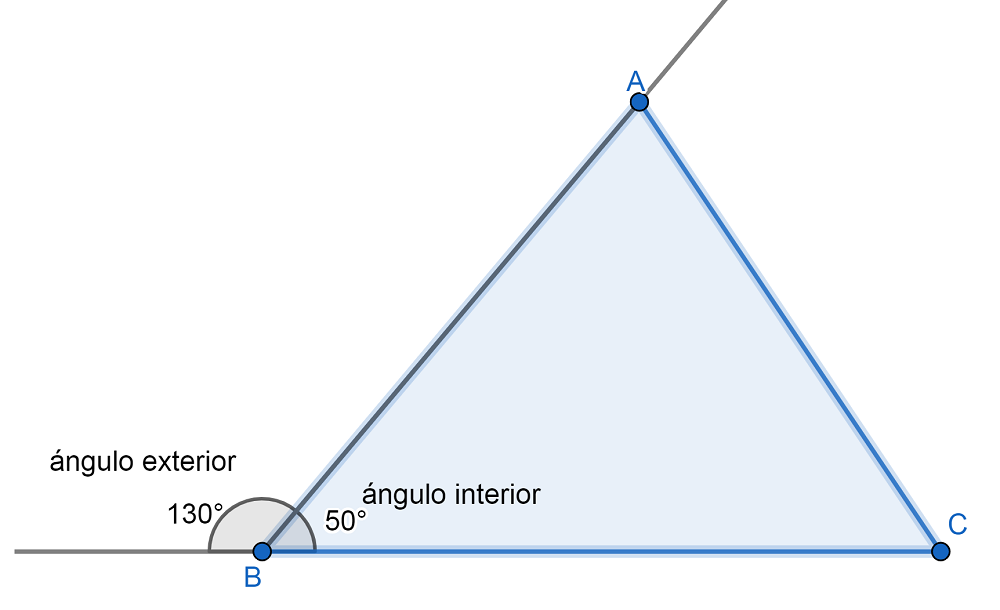
Cada vértice del polígono se corresponde con un ángulo interior y uno exterior, siendo ambos suplementarios, es decir, suman 180º.
Por ejemplo, si el ángulo interior de un triángulo es 50º, su correspondiente ángulo exterior en ese mismo vértice mide 130º.
En este punto, debemos recordar que un polígono es una figura geométrica bidimensional formado por segmentos consecutivos no colineales, constituyendo un espacio cerrado.
Cabe señalar que si alguno de los ángulos interiores de un polígono es mayor a 180º o π radianes, el polígono es cóncavo. En cambio, si todos los ángulos interiores son menores a 180º, el polígono es convexo (ver imagen inferior).
Asimismo, si todos los ángulos interiores de un polígono son iguales nos encontramos frente a un polígono equiangular.
Suma y medida de los ángulos interiores
Para saber cuánto suman los ángulos interiores de un polígono simple (sus lados no se cruzan entre sí), debemos seguir la siguiente fórmula.
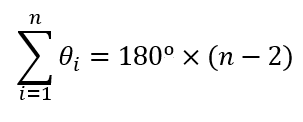
En la imagen superior, n es el número de lados de lados del polígono y θ es el ángulo interior.
Asimismo, teniendo un polígono regular, que es aquel cuyos lados y ángulos interiores miden lo mismo, la medida de cada ángulo interior podrá ser calculada con esta fórmula:
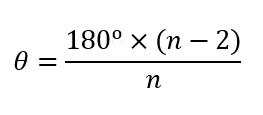
Ejemplo de ángulo interior
Supongamos que nos encontramos frente a un pentágono regular. ¿Cuánto sumarán sus ángulos internos y cuánto medirá cada uno de dichos ángulos?
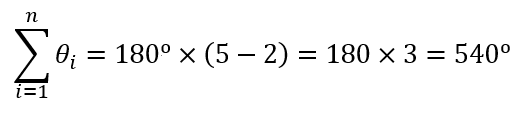
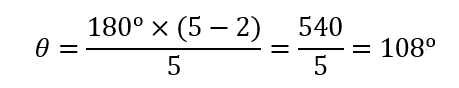
Es decir, la suma de los ángulos interiores de un pentágono es 540º , y si el polígono es regular, cada ángulo interior medirá 108º.
