Operaciones con vectores
Las operaciones matemáticas que pueden aplicarse a las coordenadas de los vectores son la suma, resta y multiplicación por un escalar.
En otras palabras, las operaciones matemáticas que pueden hacerse a las coordenadas de los vectores son la suma, la resta y la multiplicación por un número.
Suma de vectores
Para sumar dos o más vectores, tendremos que sumar las coordenadas de forma que coincida el eje para cada coordenada de los vectores. La primera coordenada corresponde al eje X y la segunda coordenada corresponde al eje Y. Entonces tendremos que operar las coordenadas que coincidan en eje. Esquemáticamente:
- Las coordenadas vinculadas al eje X para los siguientes vectores son la coordenada “a” para el vector v y la coordenada “c” para el vector x.
- Las coordenadas vinculadas al eje Y para los siguientes vectores son la coordenada “b” para el vector v y la coordenada “d” para el vector x.
El nuevo vector será la suma de los siguientes vectores o también puede definirse como un vector nuevo:
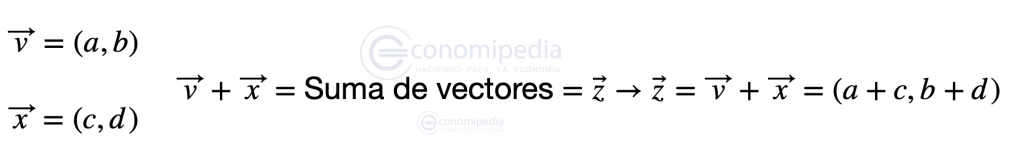
La suma de los vectores será la suma de sus coordenadas respetando el eje al que pertenecen. Podemos ver como la primera coordenada del vector suma es la suma de las primeras coordenadas de los vectores (a y c). La segunda coordenada del vector suma es la suma de las segundas coordenadas de los vectores (b y d).
Resta de vectores
Para restar dos o más vectores, tendremos que restar las coordenadas de forma que coincida el eje de cada coordenada de los vectores.
La primera coordenada corresponde al eje X y la segunda coordenada corresponde al eje Y. Entonces tendremos que operar las coordenadas que coincidan en eje. Esquemáticamente:
- Las coordenadas vinculadas al eje X para los siguientes vectores son la coordenada “a” para el vector v y la coordenada “c” para el vector x.
- Las coordenadas vinculadas al eje Y para los siguientes vectores son la coordenada “b” para el vector v y la coordenada “d” para el vector x.
El nuevo vector será la resta de los siguientes vectores o también puede definirse como un vector nuevo:

La resta de los vectores será la resta de sus coordenadas respetando el eje al que pertenecen. Podemos ver como la primera coordenada del vector resta es la resta de las primeras coordenadas de los vectores (a y c). La segunda coordenada del vector resta es la resta de las segundas coordenadas de los vectores (b y d).
Multiplicación por un escalar
La multiplicación de un vector por un número (escalar) se completa haciendo el producto de dicho número por las coordenadas del vector. El nuevo vector será la multiplicación del vector por el escalar o también puede definirse como un vector nuevo:

Ejemplo de operaciones con vectores
Suma, resta y multiplica por un escalar los siguientes vectores:

