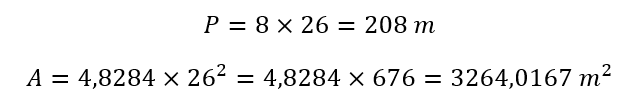Octógono
El octógono es una figura geométrica formada por ocho lados. A su vez, posee ocho vértices y ocho ángulos internos.
Es decir, el octógono es un polígono que cuenta con ocho lados, por lo que es más complejo que un hexágono o un heptágono.
Cabe recordar que un polígono es una figura bidimensional constituida por un grupo de segmentos consecutivos (no colineales), que forman un espacio cerrado.
Elementos del octógono
Tomando como referencia imagen inferior, los elementos del octógono son los siguientes:
- Vértices: A, B, C, D, E, F, G, H.
- Lados: AB, BC, CD, DE, EF, FG, GH y AH.
- Ángulos interiores: α, β, δ, γ, ε, ζ, η, θ. Suman 1080º.
- Diagonales: Son 20 y parten en 5 de cada ángulo interior: AC, AD, AE, AF, AG, BD, BE, BF, BG, BH, CF, CG, CE, CH, DF, DG, DH, EG, EH, FH.
Tipos del octógono
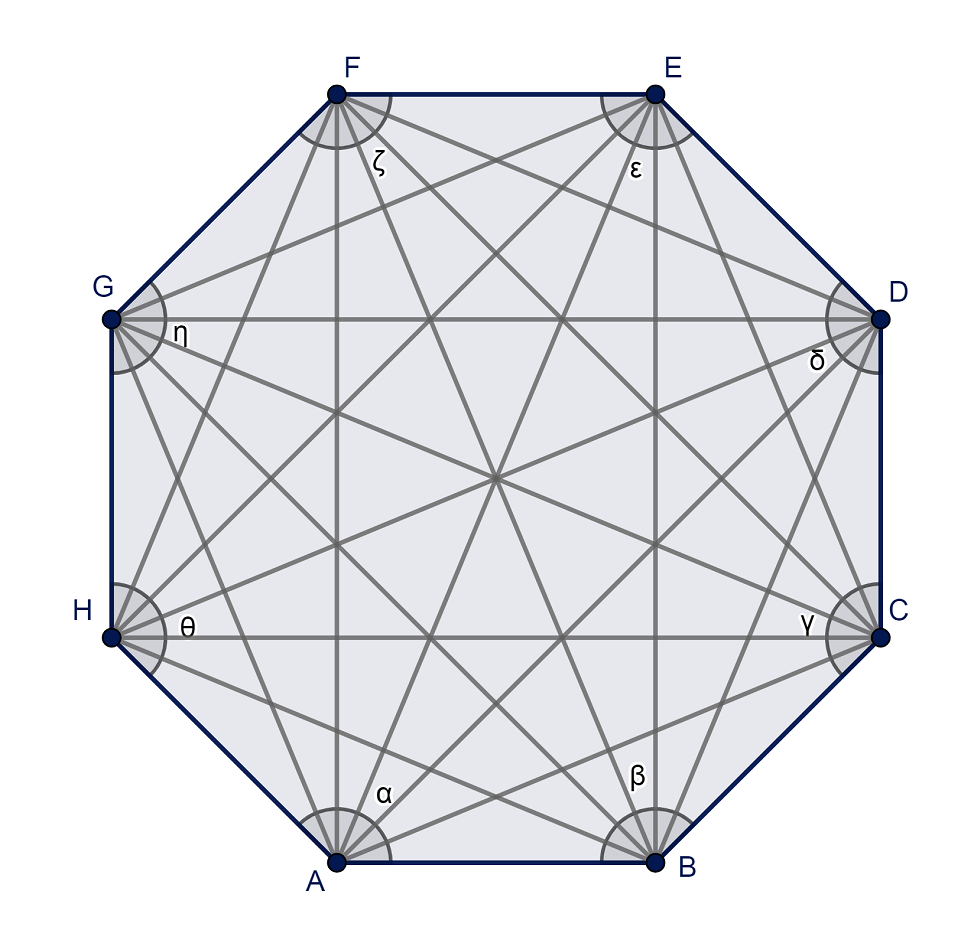
Según su regularidad, se pueden distinguir dos tipos de octógonos:
- Irregulares: Sus lados (y sus ángulos internos) miden distinto.
- Regulares: Sus lados miden igual, así como sus ángulos interiores que son de 135º.
Perímetro y área del octógono
Para saber las medidas de un octógono, podemos calcular:
- Perímetro(P): Sumamos los lados del polígono. Es decir → P= AB + BC + CD + DE + EF + FG + GH + AH. Cuando la figura es regular, solo se debe multiplicar la longitud de lado (L) por 8: P=8xL
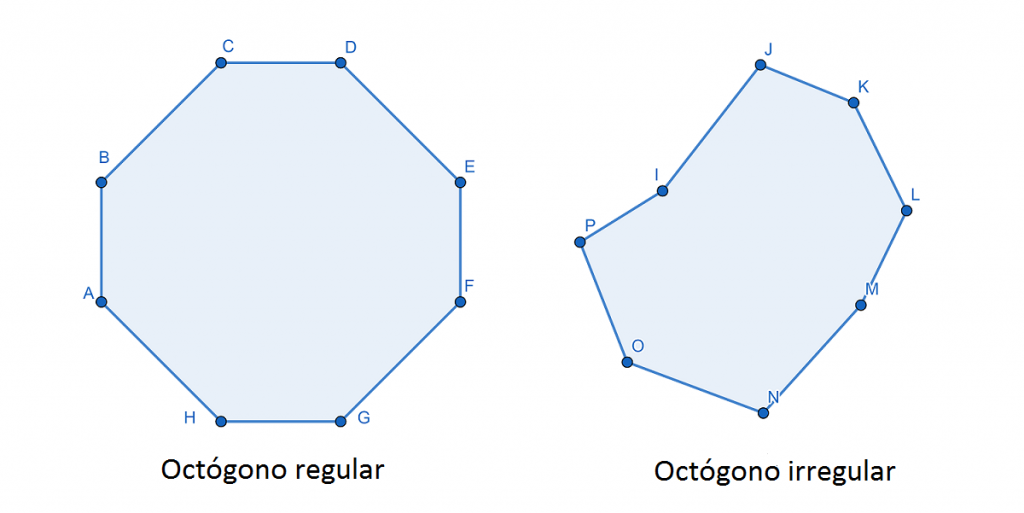
- Área(A): También podemos distinguir dos casos. Cuando la figura es irregular, se puede dividir en distintos triángulos (ver imagen inferior). Si conocemos la longitud de las diagonales trazadas, podemos hallar el área de cada triángulo (siguiendo los pasos que explicamos en el artículo de triángulo) y hacemos la sumatoria.
Si el octógono es regular, multiplicamos el perímetro por la apotema (a) y dividimos entre dos, como vemos en la siguiente fórmula.
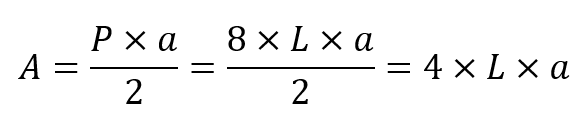
La apotema es la recta que va desde el centro de un polígono regular hasta el punto medio de cualquiera de sus lados. La intersección entre la apotema y el lado del polígono forma un ángulo recto (que mide 90ª). Entonces, es posible expresar la apotema como una función de la longitud del lado de la figura.
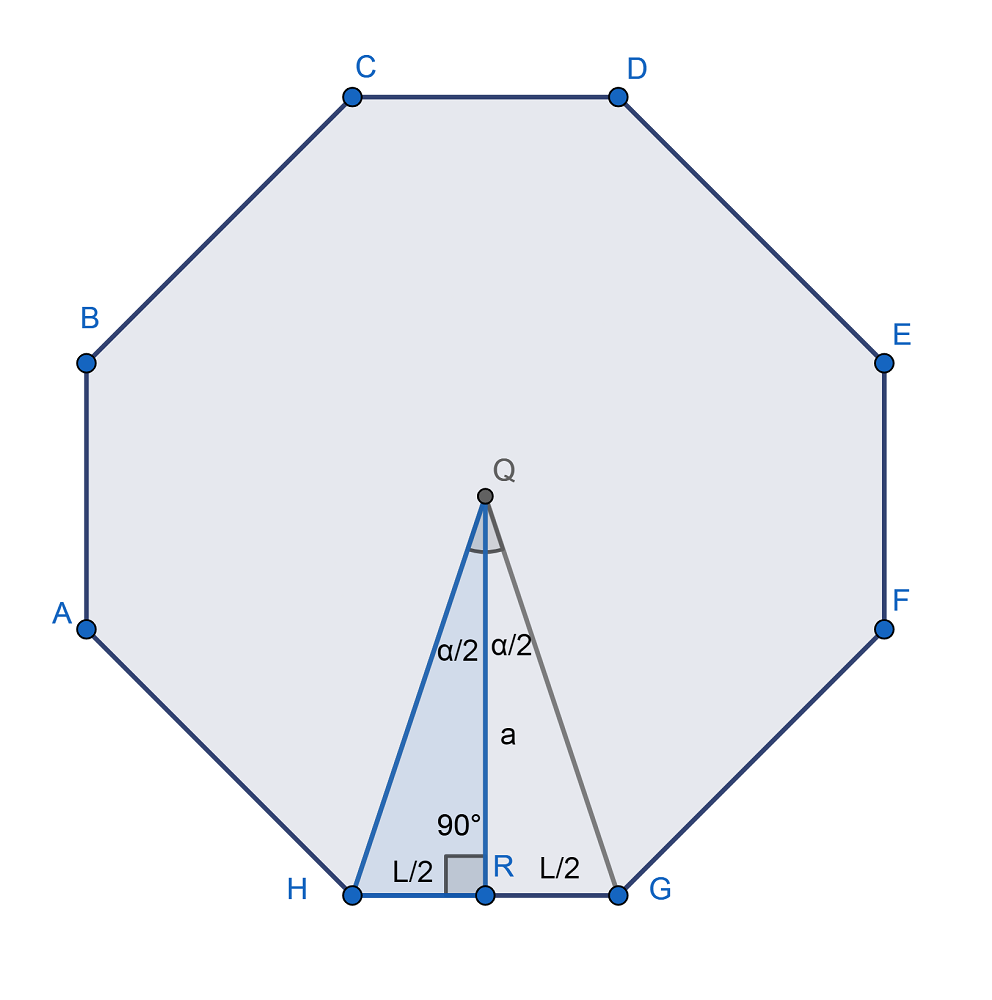
Primero, observemos que el ángulo central (α) en el octógono resulta de dividir 360º entre 8. Es decir, es igual a 45º. Luego, si observamos el triángulo QHR, notamos que es un triángulo rectángulo. Su hipotenusa es QH (Q es el punto medio de la figura), y los catetos son L/2 (la mitad de la longitud del lado) y la apotema (a). Asimismo, α/2 es 22,5º (45/2). Ahora, sabemos que la tangente (tan) del ángulo de un triángulo rectángulo (en este caso el ángulo α/2) es igual al cateto opuesto (L/2) entre el cateto adyacente que es la apotema (a) y lo resolvemos de la siguiente forma:
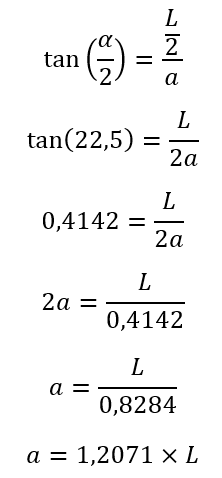
Luego reemplazamos a en la fórmula del área (A):
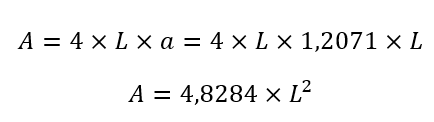
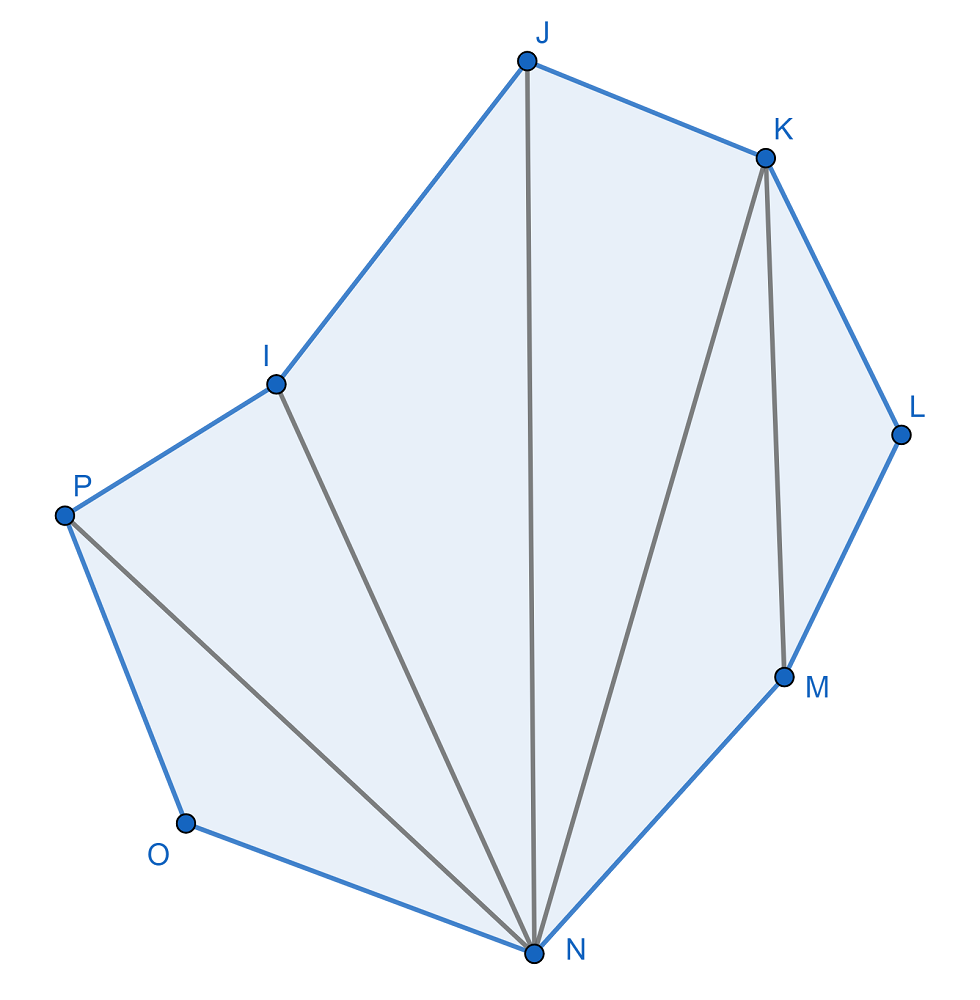
Ejemplo de octógono
Imaginemos que tenemos un octógono regular con un lado que mide 26 metros. ¿Cuál es su perímetro y su área?