Modelos de elección binaria
Los modelos de elección binaria son modelos donde la variable dependiente sólo toma dos valores: 1 para indicar «éxito» o «0» para indicar fracaso. Los modelos concretos de estimación son: probabilidad lineal, logit y probit.
En el modelo de regresión simple o múltiple que es enseñado en el curso introductorio de Econometría, la variable dependiente suele tener una interpretación económica (como el incremento del PIB, la inversión o el consumo) a partir de otras variables explicativas.
Pero, ¿qué modelo utilizamos cuando queremos explicar eventos que sólo tienen dos posibilidades? Por ejemplo: aprobar la materia o no aprobarla, graduarse de la universidad o no graduarse, estar empleado o desempleado, etc. A esto es a lo que dan respuesta los modelos de elección binaria.
En cada uno de estos casos se puede hacer que y = 1 denote “éxito”; y = 0 denote “fracaso”. Por este motivo se denominan modelos de elección binaria y la ecuación que utiliza es así:
De este modo obtendremos la probabilidad de éxito de una determinada variable.
Hasta ahora no tiene mayor complicación. Sin embargo, la estimación e interpretación de los parámetros requiere mayor cuidado.
Modelos para estimar los parámetros binarios
Dadas las características ya mencionadas de la variable independiente, existen tres modelos para la estimación de los parámetros:
- Modelo de probabilidad lineal. Se calcula a través de MCO normal.
- Modelo logit. Se calcula con una función de distribución logística estándar.
- Modelo probit. Se calcula con una función de distribución normal estándar.
Modelo de probabilidad lineal
El modelo de probabilidad lineal (MPL) se llama así porque la probabilidad
de respuesta es lineal con respecto a los parámetros de la ecuación. Para la estimación utiliza mínimos cuadrados ordinarios (MCO)
La ecuación estimada se escribe
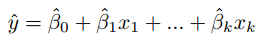
La variable independiente (y gorro) es la probabilidad de éxito predicha.
El B0 gorro es la probabilidad de éxito predicha cuando cada una de las x es igual a cero. El coeficiente B1 gorro mide la variación de la probabilidad de éxito predicha cuando x1 aumenta una unidad.Para interpretar correctamente un modelo de probabilidad lineal, debemos tener en cuenta qué se considera un éxito y que no.
Ejemplo de modelo de de elección binaria
El economista Jeffrey Wooldridge hizo una estimación de un modelo econométrico donde la variable binaria indica si una mujer casada participó en la fuerza laboral (variable explicada) durante 1975. En este caso y = 1 significaba que participó e y = 0 que no lo hizo.
El modelo utiliza como variables explicativas el nivel de ingresos del esposo (hinc), los años de educación (educ), los años de experiencia en el mercado laboral (exper), la edad (age), la cantidad de hijos menores de seis años (kidslt6) y la cantidad de hijos entre 6 y 18 años (kidsge6).
Podemos comprobar que todas las variables, excepto kidsge6 son estadísticamente significativas y todas las variables significativas tienen el efecto esperado.
Ahora bien, la interpretación de los parámetros es así:
- Si aumenta un año de educación, ceteris paribus, la probabilidad de formar parte de la fuerza laboral se incrementa en 3.8%.
- En caso de que aumente en un año la experiencia, la probabilidad de formar parte de la fuerza laboral se incrementa en 3.9%.
- Si tiene un hijo menor 6 años, ceteris paribus, la probabilidad de formar parte de la fuerza laboral se disminuye en 26.2%.
Entonces, vemos que este modelo nos indica el efecto de cada situación sobre la probabilidad de que una mujer esté contratado formalmente.
Este modelo se puede utilizar para evaluar políticas públicas y programas sociales, debido a que se puede cuantificar el cambio en la “probabilidad de éxito predicha” con respecto a cambios unitarios o marginales en las variables explicativas.
Inconvenientes del modelo de probabilidad lineal
Sin embargo, este modelo tiene dos inconvenientes principales:
- Puede dar probabilidades menores a cero y mayores a uno, lo cual no tiene sentido en términos de interpretar dichos valores.
- Los efectos parciales son siempre constantes. En este modelo no hay diferencia entre pasar de cero hijos a un hijo, que pasar de dos a tres hijos.
- Como la variable explicativa sólo toma valores de cero o uno, se puede generar heterocedasticidad. Para solucionar esto se usan errores estándar.
Para resolver los primeros dos problemas, que son los más importantes del modelo de probabilidad lineal, se diseñaron los modelos Logit y Probit.
Referencias:
Wooldridge, J. (2010) Introducción a la Econometría. (4ª ed.) México: Cengage Learning.
