Modelo VAR

En otras palabras, el Modelo VAR es un modelo de predicción para diversas variables en un solo modelo a través de un vector de k regresiones temporales con p·k variables independientes rezagadas (autorregresivo). 

Artículos recomendados:  ADR (I), ADR (II), operaciones con matrices, AR(1). 

El modelo VAR transforma la autorregresión univariante (autorregresión con una sola variable) a múltiples variables temporales en forma de vector.  

El modelo VAR depende del número de regresores y variables rezagadas en cada regresión temporal k. Entonces, podemos expresar el modelo VAR de la forma: VAR(p). 

Modelo AR(p) es la base del modelo VAR:

El modelo VAR es una extensión del modelo ADR(p,q):

Para simplificar la comprensión, reducimos el modelo VAR a dos ecuaciones, tal que, VAR(p) con 2 regresiones temporales (k=2) y con 2 variables rezagadas, X_te Y_t:

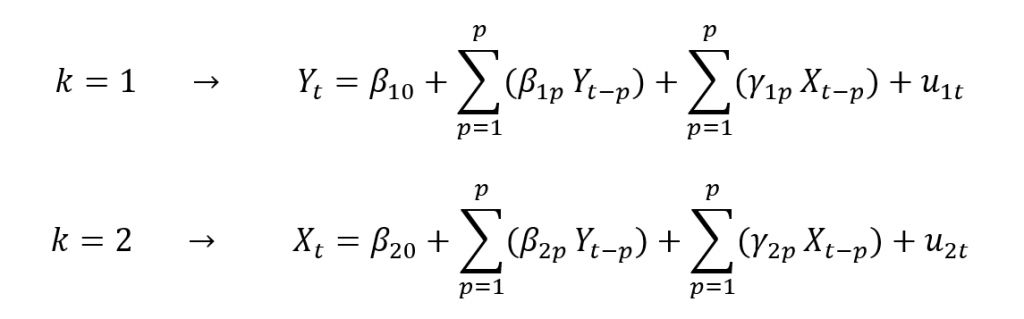
k: Número de regresiones temporales.

p: Número de variables rezagadas en cada regresión temporal k.

Se utilizan distintas letras griegas en los regresores (beta y gamma) para poder diferenciar los regresores de cada variable. Se podrían utilizar ß en todas las variables indistintamente. 

¡Que no cunda el pánico! ¿Qué podemos ver a primera vista de estas regresiones?

• Encontramos el significado de vector autorregresivo: los vectores son

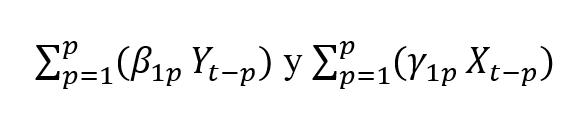
ya que podrían expresarse de la forma vectorial (V):

• Todas las variables de todas las regresiones están rezagadas. Es decir, retroceden p períodos en el tiempo. Si suponemos que estamos en tiempo t, entonces retroceder p períodos equivale a t-p:

Los regresores del modelo VAR se estiman mediante Mínimos Cuadrados Ordinarios (MCO). 

En economía, el modelo VAR se emplea para hacer pronósticos mediante varias variables en un solo modelo con el objetivo de hacer las pronósticos mutuamente consistentes.

Suponemos que queremos estudiar el precio de los forfaits para esta temporada 2019 (t) en función de los precios de los forfaits y del número de pistas negras abiertas de las temporadas anteriores 2018 y 2017. Entonces, en vez de utilizar el modelo AR(p) o ADR(p,q) podemos utilizar el modelo VAR(p).

• Descargamos los datos sobre los precios de los forfaits(F_t) y pistas negras (PN_t). 

Año	Forfaits (€)	ln_t	ln_t-1	ln_t-2	PN_t	PN_t-1	PN_t-2
2007	88	4,477			6
2008	40	3,688	4,477		5	6
2009	68	4,219	3,688	4,477	6	5	6
2010	63	4,143	4,219	3,688	10	6	5
2011	69	4,234	4,143	4,219	6	10	6
2012	72	4,276	4,234	4,143	8	6	10
2013	75	4,317	4,276	4,234	8	8	6
2014	71	4,262	4,317	4,276	5	8	8
2015	73	4,290	4,262	4,317	9	5	8
2016	63	4,143	4,290	4,262	10	9	5
2017	67	4,204	4,143	4,290	8	10	9
2018	68	4,219	4,204	4,143	6	8	10
2019	?	?	4,219	4,204	?	6	8

1. Vamos a realizar la predicción mediante el modelo VAR(p). 

Queremos retroceder 2 años atrás, entonces, p=2, y tenemos dos variables, forfaits(F_t) y pistas negras (PN_t), entonces, k=2. 

VAR(2):

• Estimación mediante MCO obtenemos:

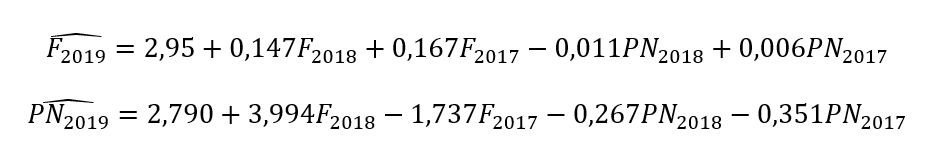
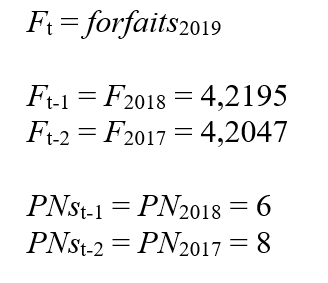
Entonces,

Año	Forfaits (€)	ln_t	ln_t-1	ln_t-2	PN_t	PN_t-1	PN_t-2
2007	88	4,477				6
2008	40	3,688	4,477		6	5
2009	68	4,219	3,688	4,477	6	6
2010	63	4,143	4,219	3,688	6	5	10
2011	69	4,234	4,143	4,219	10	6	6
2012	72	4,276	4,234	4,143	6	10	8
2013	75	4,317	4,276	4,234	8	6	8
2014	71	4,262	4,317	4,276	8	8	5
2015	73	4,290	4,262	4,317	5	8	9
2016	63	4,143	4,290	4,262	9	5	10
2017	67	4,204	4,143	4,290	10	9	8
2018	68	4,219	4,204	4,143	8	10	6
2019	71	4,259	4,219	4,204	6	8	8

Es decir, nuestro modelo VAR pronostica que en 2019 el número de pistas negras abiertas será de 6 y, por tanto, el precio del forfait será de 71€.