Modelo de Ramsey

En el modelo de Solow se asumía que los hogares consumidores, que son al mismo tiempo productores, ahorran una tasa constante de su ingreso. Sin embargo, estos supuestos eran bastante cuestionables.

En el modelo de Ramsey se explicita que los hogares y las empresas son entidades separadas que interactúan en el mercado. Por un lado, los hogares (consumidores) son propietarios de trabajo y ciertos activos financieros; por otro lado, las empresas (productores) compran trabajo a cambio de salario y compran capital a una tasa de interés. Finalmente, los consumidores y productores se encuentran en el mercado y los precios del capital, el trabajo y el producto hace que los mercados se equilibren.

Este modelo de equilibrio general se le conoce también como CKR porque Cass (1965) y Koopmans (1965) retomaron el enfoque de optimización intertemporal introducido por Ramsey (1928) para analizar el comportamiento maximizador de los consumidores.

En lo fundamental, el modelo CKR es muy parecido al modelo de Solow. La diferencia crucial es que la tasa de ahorro se determina endógenamente.

Para ello, este modelo plantea la maximización de la función de utilidad intertemporal:

donde

• La integral de 0 a infinito significa que se trae a valor presente todos los consumos futuros (hay una noción de “generación tras generación”)
• p representa una tasa de impaciencia de consumo
• n representa la tasa de crecimiento poblacional
• u(c_t) es la función de utilidad del consumo per cápita, cuya forma generalizada se expresa en el último término de la ecuación
• theta indica la concavidad de la función y representa la aversión al riesgo.
  • Si theta=0, la función de utilidad es lineal
  • Si theta=1, la función de utilidad es logarítmica
• La restricción (s.a) indica que la acumulación neta de capital es igual al ahorro (producción menos consumo) menos la destrucción del capital (delta representa la depreciación del capital y n indica que si hay un mayor crecimiento poblacional, debe haber un mayor aprovisionamiento de capital.

El problema de maximización se soluciona a través del hamiltoniano:

Con esta solución no obtenemos un nivel exacto de consumo, sino una trayectoria de consumo que maximiza la utilidad total. Este tipo de planteamiento de maximización de una función de utilidad intertemporal será la base para la resolución de futuros modelos de crecimiento endógeno.

La dinámica del modelo CKR se puede representar con un diagrama de fase.

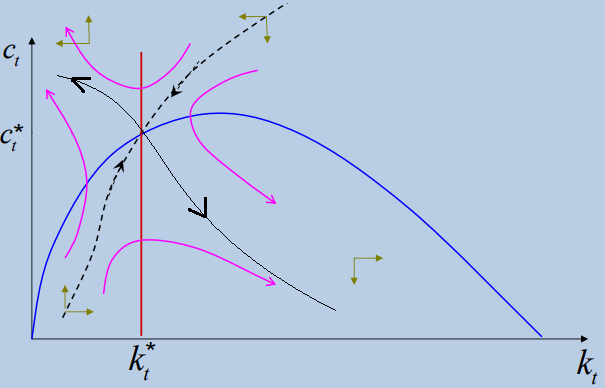
Se observa que se existe una senda por donde se converge a un estado estacionario, donde las variaciones de crecimiento del consumo y el capital per cápita son iguales a cero. Pero también hay otra senda donde se aleja cada vez más del estado estacionario. Por ello, concluimos que en este caso, el estado estacionario es un punto de silla.

Si el consumo es bajo en el presente, el ahorro presente es alto, se acumula más capital y habrá un mayor consumo en el futuro. Dicho consumo bajo se puede representar con un p (tasa de impaciencia) pequeño.

Cabe destacar que en el estado estacionario el nivel de consumo del modelo CKR es inferior al nivel de consumo del modelo de Solow. Sin embargo, ocurre lo contrario en el periodo de transición. Y como el tiempo de transición es más valorado que el de estado estacionario, entonces tenemos que el modelo CKR maximiza la utilidad total “generación tras generación”.

En un ambiente de mercado se llega al mismo resultado tanto por el lado de los hogares como el de las firmas, por ello se concluye que es un equilibrio general.

El modelo neoclásico de mercado que estudiamos anteriormente considera que todos los individuos tienen toda la información disponible y no hay externalidades de ningún tipo. Entonces, si existiera un planificador (que esté sujeto a la misma función objetivo y la misma restricción) encontramos la paradoja de que la solución de mercado competitivo es idéntica a la del planificador.

Precisamente los modelos de crecimiento endógeno, como el de Barro y Uzawa-Lucas, incluirán las externalidades y encontrarán que la solución descentralizada es distinta a la centralizada.

Referencias:

Sala-i-Martin, X. (2000) Apuntes de crecimiento económico. (2^a ed). Barcelona: Antoni Bosch.