Los números decimales y las fracciones
Un número decimal es cualquier número real que esté formado por una parte entera y otra parte decimal, las cuales están separadas por una coma.
En otras palabras, un número decimal es un número real que lo reconocemos por llevar una coma y se puede dividir entre una parte entera y una parte decimal.
Fracción
Una fracción se expresa de la forma:
Tanto el numerador como el denominador pueden ser números o funciones. Si fueran funciones que dependen de la misma variable podríamos escribirlo de la siguiente forma:
Número Decimal
Un número decimal se expresa de la forma:

Donde e es un número entero y todas las siguientes letras d significan decimal. Por tanto, en un número decimal siempre encontraremos una parte entera. La parte entera es el número anterior a la coma. La parte decimal es la parte posterior a la coma.
Esquema de la estructura de un número decimal
La parte decimal también recibe el nombre de parte fraccionaria. Entonces, sabiendo que recibe este nombre, ya podemos pensar que los números decimales y las fracciones comparten cosas.
Los números decimales y las fracciones
¿Qué tienen en común los números decimales y las fracciones?
Los números decimales y las fracciones tienen tantas cosas en común que llegan a ser el mismo concepto matemático pero con distinta expresión. En otras palabras, los números decimales y las fracciones son lo mismo pero escrito de diferente manera:
Vamos a demostrarlo
Suponemos que queremos escribir el número 4,5 en fracción.
Primero tenemos que pensar en dos números que divididos den como resultado 4,5. Esta combinación de números puede ser cualquiera. Por ejemplo, 9 y 2
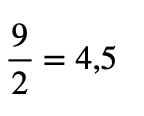
Cualquier función equivalente tendrá como resultado 4,5.
Obtenemos 4,5 por la división de 9 entre 2, tal que así:
Entonces, vemos que podemos expresar el mismo elemento numérico dos formas distintas: en forma de función y en forma de número decimal.
Ejemplo de decimales y fracciones
Expresa en fracción los siguientes números decimales:
Dadas las propiedades de las fracciones, estos tres ejemplos podrían expresarse con otras fracciones equivalentes. Por ejemplo, 3,5 puede ser la división de 14/4, de 28/8 o de 112/32. Las fracciones equivalentes son aquellas fracciones que se obtienen de multiplicar el numerador y el denominador por el mismo número.
La solución del primer ejemplo es la fracción de 7/2 ya que es la fracción irreductible. En otras palabras, es una fracción que no puede reducirse más de forma equivalente para que tenga como resultado un entero para el dividendo y el divisor.
