Función de probabilidad de la distribución de Bernoulli
La distribución de Bernoulli es un modelo teórico utilizado para representar una variable aleatoria discreta la cual solo puede finalizar en dos resultados mutuamente excluyentes.
Artículos recomendados: distribución de Bernoulli, ejemplo Bernoulli, espacio muestral y Regla de Laplace.
Función de probabilidad Bernoulli
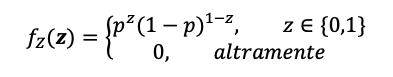
Definimos z como la variable aleatoria Z una vez conocida y fijada. Es decir, Z va cambiando aleatoriamente (el dado gira y gira en un único lanzamiento) pero cuando la observamos fijamos el valor (cuando el dado cae encima de la mesa y da un resultado concreto). Es en ese momento cuando evaluamos el resultado y le asignamos uno (1) o cero (0) en función de lo que consideremos “éxito” o no “éxito”.
La variable aleatoria Z una vez fijada solo podrá tomar dos valores concretos: cero (0) o uno (1). Entones, la función de distribución de probabilidad de la distribución de Bernoulli solo será distinta de cero (0) cuando z sea cero (0) o uno (1). El caso contrario sería que la función de distribución de la distribución de Bernoulli fuera cero (0) dado que z será cualquier valor distinto de cero (0) o uno (1).
La función anterior también puede reescribirse como:
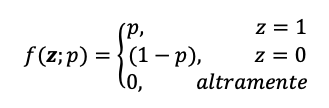
Si sustituimos z = 1 en la primera fórmula de la función de probabilidad veremos que el resultado es p que coincide con el valor de la segunda función de probabilidad cuando z=1. Del mismo modo, cuando z=0 obtenemos (1-p) para cualquier valor de p.
Momentos de la función
Los momentos de una función de distribución son valores específicos que registran la medida de distribución en distintos grados. En este apartado solo mostramos los primeros dos momentos: la esperanza matemática o valor esperado y la varianza.
Primer momento: valor esperado.
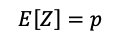
Segundo momento: varianza.
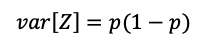
Ejemplo de momentos de Bernouilli
Suponemos que queremos calcular los dos primeros momentos de una distribución de Bernoulli dada una probabilidad p = 0,6 tal que
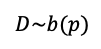
Donde D es una variable aleatoria discreta.
Entonces, sabemos que p = 0,6 y que (1-p) = 0,4.
- Primer momento: valor esperado.
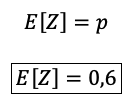
Segundo momento: varianza.
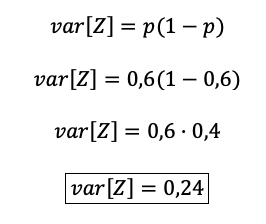
Además, queremos calcular la función de distribución dada la probabilidad p = 0,6. Entonces:
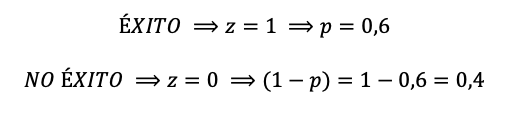
Dada la función de probabilidad:
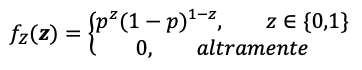
Cuando z = 1

Cuando z = 0

El color azul indica que las partes que coinciden entre ambas formas (equivalentes) de expresar la función de distribución de probabilidad de la distribución de Bernoulli.
