Estimador consistente

De la definición de estimador insesgado, podemos extraer la conclusión de que, en ocasiones, tenemos errores de estimación. Ahora bien, existen casos en los que cuando la muestra se va haciendo más grande el error disminuye.

Algunas veces, por las características del estimador utilizado, conforme el tamaño de la muestra aumenta el error aumenta también. Ese estimador no sería deseable utilizarlo. Ahora bien, a priori, no sabemos hacia dónde tiende el sesgo. Si tiende a cero, tiende a cierto valor o tiende a infinito cuando el tamaño de la muestra se hace más grande.

Dicho esto, se hace necesario definir el concepto de consistencia. Para ellos, hemos de decir que existen dos tipos de consistencia. Por un lado, existe la consistencia simple. Mientras que, por otra parte, se encuentra la consistencia en media cuadrática.

Por decirlo de alguna manera, son dos herramientas matemáticas que nos permiten calcular hacia qué número o números converge nuestro estimador.

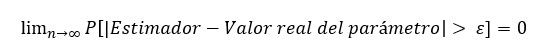
Un estimador cumple la propiedad de consistencia simple en caso de cumplir la siguiente ecuación:

De izquierda a derecha, la ecuación se lee de la siguiente manera: El límite, cuando el tamaño de muestra tiende a infinito, de la probabilidad de que la diferencia absoluta entre el valor del estimador y el valor del parámetro sea mayor que el error, es igual a cero.

Se entiende que el valor del error notado por épsilon, debe ser mayor que cero.

Intuitivamente, la fórmula indica que cuando el tamaño de la muestra se hace muy grande, la probabilidad de que exista un error mayor que cero es cero. Dicho de forma inversa, la probabilidad de que no exista error cuando el tamaño de la muestra es muy grande es, hablando en probabilidades, de prácticamente el 100%.

Otra herramienta que se puede utilizar para comprobar que un estimador es consistente es el error cuadrático medio. Esta herramienta matemática es aún más potente que la anterior. La razón es que la exigencia de esta condición es mayor.

En el apartado anterior, la exigencia era que, probabilísticamente hablando, la posibilidad de cometer un error fuese cero o muy cercana a cero.

Ahora, lo que estamos exigiendo lo define la siguiente igualdad matemática:

Es decir, que cuando el tamaño de muestra sea grande, la esperanza matemática de los errores al cuadrado sea cero. La única opción de que este valor sea cero, es que el error siempre valga cero. ¿Por qué? Porque al estar elevado a dos el error de estimación (Estimador – Valor verdadero del parámetro), el resultado siempre va a ser positivo. A menos, eso sí que el error sea cero. Cero elevado a dos es cero.

Claro está que, si el límite da como resultado 0,0001, podemos asumir que es igual a cero. Es casi imposible que la aplicación del error en media cuadrática salga cero.

Estadísticamente hablando diremos que un estimador es consistente en media cuadrática, en caso de que la esperanza del error al cuadrado del estimador teniendo en cuenta distintas muestras es cero o muy cercano a él.