Estimación con variables instrumentales (VI)
El método de Variables Instrumentales (VI) se utiliza para solucionar el problema de endogeneidad de una o más variables independientes en una regresión lineal.
La aparición de endogeneidad en una variable indica que esta variable está correlacionada con el término de error. En otras palabras, se ha omitido una variable que está correlacionada con las otras. Hablamos de variables explicativas que presentan correlación con el término de error. Otro método muy popular para resolver el problema de la endogeneidad es el estimador de Mínimos Cuadrados en Dos Etapas (MC2E). La función principal de VI es detectar la presencia de una variable explicativa en el término de error.
Introducción al concepto
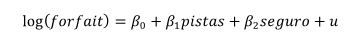
Queremos estudiar la variación de los precios de los forfaits en función del número de pistas y las aversión al riesgo de los esquiadores reflejada en la calidad del seguro. Ambas variables explicativas son variables cuantitativas.
Suponemos que incluimos la variable seguro en el término de error (u), resultando en:
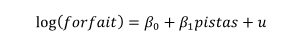
Entonces, la variable seguro se convierte en variable explicativa endógena porque pertenece al término de error y, por tanto, está correlacionado con él. Como quitamos una variable explicativa, también quitamos su regresor, en este caso, B2.
Si hubiéramos estimado este modelo con Mínimos Cuadrados Ordinarios (MCO), hubiéramos obtenido una estimación inconsistente y sesgada para B0 y Bk.
Podemos utilizar el Modelo 1.A si encontramos una variable instrumental (z) para pistas cumpliendo:
- Cov (z, u) = 0 => z no está correlacionada con u.
- Cov (z, pistas) ≠ 0 => z sí está correlacionada con pistas.
Esta variable instrumental (z) es exógena al Modelo 1 y, por tanto, no tiene ningún efecto parcial sobre log(forfaits). Aún así, es relevante para explicar la variación en pistas.
Contraste de hipótesis
Para saber si estadísticamente la variable instrumental (z) está correlacionada con la variable explicativa (pistas), podemos probar la condición Cov(z,pistas) ≠ 0 dada una muestra aleatoria de la población. Para ello tenemos que hacer la regresiación entre pistas y z. Utilizamos una nomenclatura distinta para diferenciar sobre qué variables se está regresando.
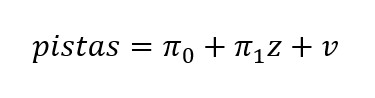
Interpretamos a los π0 y πk de la misma manera que las B0 y Bk en las regresiones convencionales.
Entendemos π1 = Cov (z,pistas) / Var(z)
- Definición de la hipótesis
En este contraste queremos probar si se puede rechazar π1 = 0 a un nivel de significación suficientemente pequeño (5%). Por tanto, si la variable instrumental (z) está correlacionada con la variable explicativa (pistas) y poder rechazar H0.
2. Estadístico de contraste
3. Regla de rechazo
Determinamos el nivel de significación al 5%. Por tanto, nuestra norma de rechazo se basará en | t | > 1,96.
- | t | > 1,96: rechazamos H0. Es decir, rechazamos no correlación entre z y pistas.
- | t | < 1,96: no tenemos suficientes evidencias significativas para rechazar H0. Es decir, no rechazamos que no exista correlación entre z y pistas.
4. Conclusión
Si concluimos que π1 = 0, estadísticamente la variable instrumental (z) no es buena aproximación para la variable endógena.
