Espacio probabilístico

En estadística, un espacio probabilístico está compuesto por varios elementos. Estos elementos los veremos más adelante. Ahora bien, en primer lugar, es necesario entender el concepto de una forma sencilla.

Cuando queremos estudiar un experimento aleatorio, lo que estamos diciendo es que pretendemos estudiar un evento dominado por el azar. Por ejemplo, el lanzamiento de un dado. Cuando estudiamos un evento aleatorio, cabe a su vez, definir tres conceptos:

• Espacio muestral.
• Sigma álgebra.
• Función de probabilidad.

Estos tres elementos son los que conforman un espacio probabilístico. Así pues, todos los eventos aleatorios que queramos estudiar, deben tener un espacio probabilístico que nos permitan estudiarlos. A continuación, vamos a desglosar cada uno de sus componentes.

Es importante, antes que nada, entender que un espacio probabilístico es una herramienta. Concretamente, una herramienta matemática que nos va a ayudar a calcular la probabilidad de determinados sucesos de un experimento aleatorio. Por ser específicos, el espacio de probabilidad nos aporta un marco. Los componentes de un espacio probabilístico son:

• Espacio muestral: Se trata de todos los posibles resultados de un experimento. Dicho de forma técnica, está compuesto por todos los sucesos elementales. Por ejemplo, el experimento de lanzar un dado una vez sobre una mesa, está compuesto por los siguientes sucesos elementales: 1,2,3,4,5 y 6.
• Sigma álgebra: Es un conjunto de conjuntos sobre el que se define el espacio.
• Función de probabilidad: Es la función matemática que nos permitirá calcular la probabilidad de ciertos sucesos. Por ejemplo, el suceso de que, al lanzar un dado una vez sobre una mesa, salga mayor que 3.

La mejor forma de explicar un concepto tan abstracto como este, es con un ejemplo. Es cierto que se trata de un concepto matemático complejo. Sin embargo, también se trata de un concepto de suma importancia en la teoría de la probabilidad.

Dicho esto, supongamos, como hemos hecho hasta ahora, un ejemplo muy sencillo: el lanzamiento de un dado de tres caras. A menos que el dado esté trucado o sea imperfecto, se trata de un evento puramente aleatorio. Si lanzamos el dado en las mismas condiciones durante millones de veces, el resultado debe ser que la probabilidad que salga cualquier número es igual para todos los números. Bajo este precepto, formulemos el ejemplo mediante un ejercicio resuelto.

El experimento aleatorio consiste en tirar un dado una vez sobre una mesa en 1000 ocasiones. Así pues, tendremos 1000 resultados. Sabiendo esto, y suponiendo como lo hemos hecho, que el dado es perfecto y las condiciones de lanzamiento son las mismas, ¿cuál es el espacio de probabilidad?

Empecemos recordando, que el espacio probabilístico se divide en tres componentes. De tal forma que iremos completando cada uno de ellos por separado:

• Ω (Omega): Esta es la letra griega con la que designaremos el espacio muestral. El espacio muestral está compuesto por todos los sucesos elementales del experimento. Es decir, está compuesto por:
  • 1: Sale el número uno cuando lanzamos el dado.
  • 2: Sale el número dos cuando lanzamos el dado.
  • 3: Sale el número tres cuando lanzamos el dado.
• σ-Álgebra: {Ø,{1},{2},{3},{1,2},{1,3},{3,2},{1,2,3}}.
• Función de probabilidad ↓

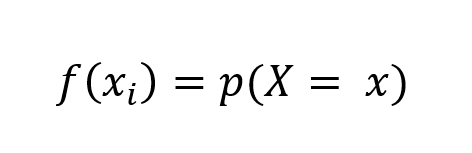
Aunque no atañe a este artículo calcular la probabilidad, explicaremos esta última función. La probabilidad de que salga 2, se expresaría como → f(2) = p(X = 2). Como la probabilidad de que salga cualquiera de las tres posibilidades es la misma, la probabilidad de salir 2 es 1/3.