Diferencia entre función y ecuación

En otras palabras, la diferencia entre una función y una ecuación depende del poder que tengamos para dar valores a las variables y de la capacidad de representación.

Una ecuación se caracteriza por hacer de puente entre dos expresiones matemáticas. Dicho puente es el símbolo matemático que conocemos por igual (=) y, como su nombre indica, representa la igualdad. Existen ecuaciones en las que el puente no es (=), sino que son desigualdades que pueden ser completas (> , <) o parciales (≥ , ≤). En el caso que el puente no sea una igualdad (=) hablaremos de inecuaciones.

Para que sea más fácil recordar que es una ecuación, podemos recurrir a su traducción al inglés. La palabra “igual” (=) traducida al inglés sería “equal”. Puede que sea más fácil recordar “equal” ya que se parece más a la palabra “ecuación” y, por tanto, saber que estamos hablando del símbolo (=).

Entonces, para las inecuaciones, ya que existe el prefijo negativo delante (in-ecuaciones), es parecido a decir no ecuaciones, por tanto, “no igual”. En relación a esto, los símbolos matemáticos que podremos encontrar serán: > , < , ≥ , ≤.

Una función se parece a una ecuación en el sentido de entender el concepto como un puente, pero en este caso el puente será de asignación o dependencia. No hablaremos de igualdad o desigualdad, ya que cuando tengamos una función aparecerá un igual.

Las funciones se identifican por tener una “f(variables independientes)” en la ecuación. En las funciones diferenciaremos la tipología de las variables dependiendo de si son independientes o dependientes:

• Variable independiente (x): puede tomar cualquier valor que nos venga a la cabeza.
• Variable dependiente (f(x)): está limitada por el valor de la variable dependiente.

Generalmente, para cada valor de la variable independiente X solo le corresponde un único valor de la variable dependiente f(X).  Esta afirmación es cierta siempre y cuando no tengamos en cuenta otros tipos de funciones que permitan a la variable dependiente f(X) tener más de un valor de la variable independiente X asociado.

	Ecuación	Función
Asignación	Las soluciones de las variables están acotadas por la ecuación.	Las variables independientes pueden tomar cualquier valor y las variables dependientes dependen de dichos valores.
Representación	Solo se pueden representar las soluciones de la ecuación.	Se pueden representar los puntos que queramos mediante la asignación de valores a las variables independientes de la función.

Determina si los elementos de la siguiente lista son funciones o ecuaciones:

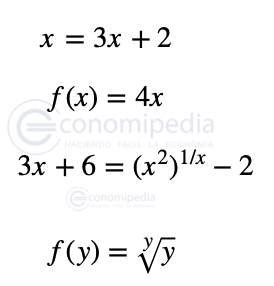
La respuesta por orden sería: ecuación, función, ecuación, función.