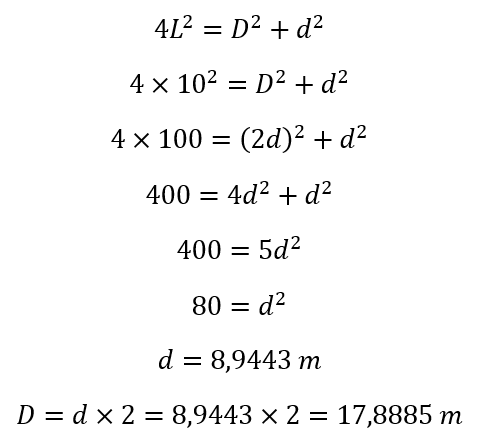Diagonal de un rombo

Para explicarlo de forma más simple, las diagonales unen cada vértice con aquel que está al lado opuesto, cortándose en el centro de la figura.

Una de las características de las diagonales de un rombo es que son perpendiculares. Es decir, al cruzarse, forman cuatro ángulos rectos o de 90º.

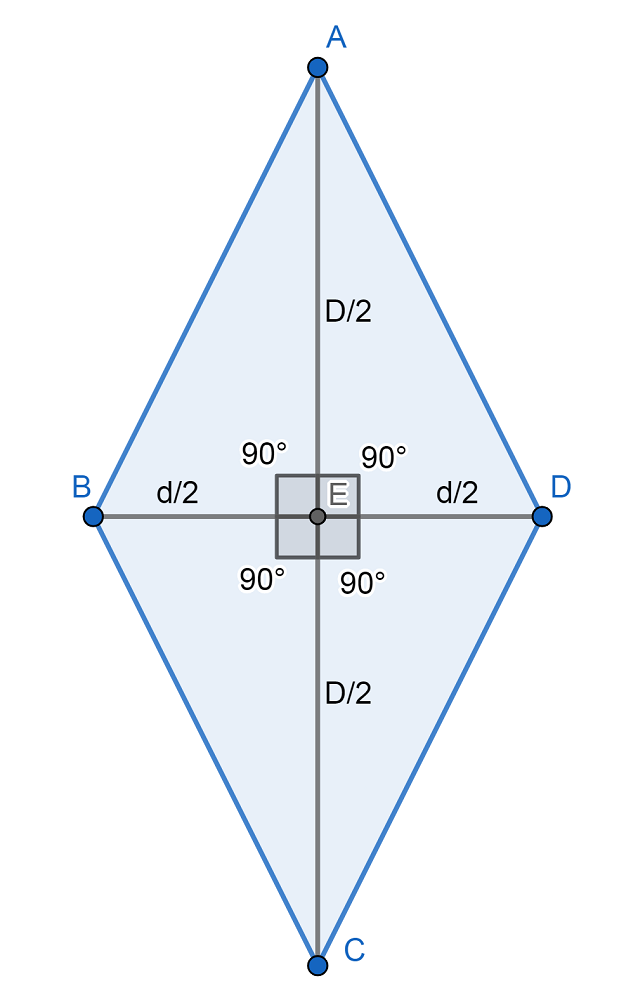
En la siguiente figura, las diagonales son los segmentos AC y DB.

Otra característica importante a tener en cuenta es que cada cada rombo tiene dos diagonales, una de mayor medida que otra. Por esa razón, una se llama diagonal mayor, mientras que la otra, diagonal menor. Esto, a diferencia de los cuadrados o los rectángulos donde las dos diagonales miden igual.

Cabe recordar que el rombo es un cuadrilátero (polígono de cuatro lados) que se caracteriza por tener todos sus lados de la misma longitud. Sin embargo, sus ángulos internos no son todos iguales, sino que hay dos pares de ángulos agudos (menores de 90º), que mide igual, y otro par de ángulos obtusos (mayores de 90º), que también son idénticos.

El rombo es, a su vez, un tipo muy particular de cuadrilátero llamado paralelogramo, que se caracteriza por tener sus lados opuestos paralelos. Es decir, no se cruzan ni en sus prolongaciones. Otro tipo de paralelogramo es el cuadrado, el rectángulo y el romboide.

Para calcular la diagonal de un rombo, debemos tomar en cuenta que, al trazar ambas diagonales, estas quedan divididas en dos partes iguales.

Entonces, se forman cuatro triángulos rectángulos (que tienen un ángulo de 90º). Al observar cualquiera de ellos, notamos que la hipotenusa es el lado del rombo, mientras que un cateto es la diagonal mayor dividida entre dos, y el otro cateto, la diagonal menor dividida entre dos.

Volviendo a la imagen de arriba, si observamos el triángulo AED, el segmento AD es la hipotenusa. En tanto, los segmentos AE y ED son los catetos, siendo el primero la mitad de la diagonal mayor (D/2) y el segundo, la mitad de la diagonal menor (d/2).

Tomando estos datos en cuenta, podemos aplicar el teorema de Pitágoras que nos indica que la hipotenusa elevada el cuadrado es igual a la suma de cada uno de los catetos elevado el cuadrado:

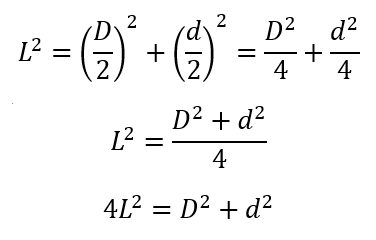
Teniendo esta fórmula en cuenta, podemos calcular la diagonal de un rombo, cuando conocemos la medida de la otra diagonal y del lado de la figura.

Supongamos que sabemos que el perímetro de un rombo mide 40 metros y su diagonal mayor mide el doble que su diagonal menor. ¿Cuánto mide cada una de las diagonales de la figura?

Primero, recordamos que el perímetro es igual a la longitud del lado multiplicada por cuatro:

Luego, despejamos en la ecuación mostrada arriba: