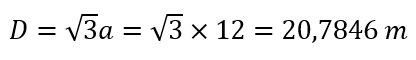Diagonal de un cubo
La diagonal de un cubo es aquel segmento que une una arista del poliedro con un vértice en la cara opuesta. Esto, de forma oblicua.
Es decir, la diagonal de un cubo es una línea inclinada que une las aristas de dos caras opuestas de la figura.
Todo cubo tiene cuatro diagonales, como observamos en la figura inferior, donde las diagonales son HC, EB, AF y DG.
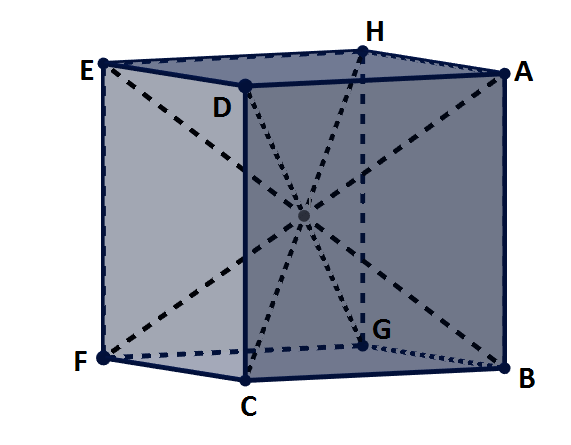
Cabe recordar que el cubo o hexaedro regular es un poliedro regular de seis caras, conformado por seis cuadriláteros idénticos entre sí. Dichos cuadriláteros, a su vez, son cuadrados. Es decir, polígonos regulares de cuatro lados, con todos los lados y ángulos interiores iguales.
Cómo calcular la diagonal de un cubo
La diagonal de un cubo se puede calcular usando el teorema de Pitágoras. Esto, tomando en cuenta que, como vemos en la figura de abajo, en el triángulo sombreado AGC, se forma un triángulo rectángulo con la diagonal del cubo (segmento AG), la diagonal de la cara inferior (AC),y la arista (GC).
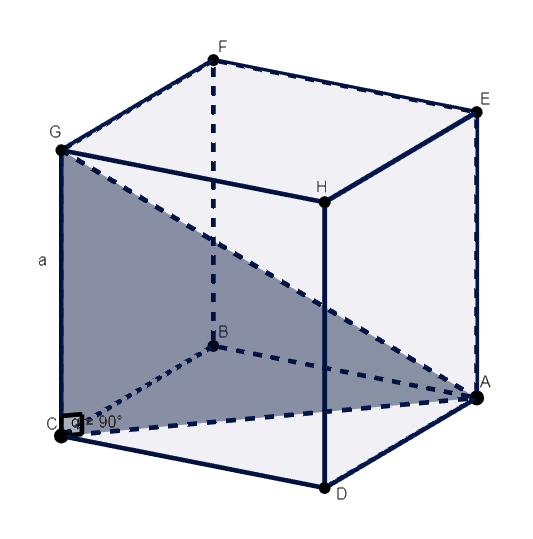
En el triángulo rectángulo AGC, el segmento AG (o D por ser la diagonal del cubo) es la hipotenusa, mientras que GC (la arista que asumiremos que mide a) y AC, son los catetos. Entonces, debemos recordar que el teorema de Pitágoras nos indica que la hipotenusa al cuadrado es igual a la suma de cada uno de los catetos al cuadrado.
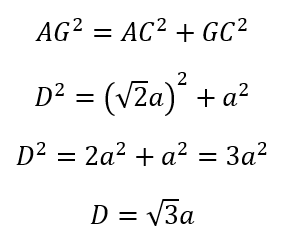
Para saber cómo calculamos el segmento AC (diagonal del cuadrado ABCD), revisar nuestro artículo sobre diagonal de un cuadrado.
Ejemplo de diagonal de un cubo
Supongamos que tenemos un cubo con una arista que mide 12 metros. ¿Cuál es la longitud de la diagonal del poliedro?