Criterio de información bayesiano

En otras palabras, queremos encontrar el número mínimo de periodos rezagados que incluimos en la autorregresión para que nos ayuden con la predicción de la variable dependiente.

De esta forma, tendremos un control sobre el número de periodos rezagados p que vamos incluyendo en la regresión. Cuando excedamos este nivel óptimo, el modelo de Schwarz dejará de disminuir y por tanto habremos llegado al mínimo. Es decir, habremos llegado al número de periodos rezagados p que minimizan el modelo de Schwarz.

También recibe el nombre de criterio de información de Bayes (BIC).

Artículos recomendados: autorregresión, suma de cuadrados de los residuos (SCE).

Aunque a simple vista parece una fórmula complicada iremos por partes para entenderla. En primer lugar, de forma general tenemos que:

• Los logaritmos en ambos factores de la fórmula representan el efecto marginal de incluir un período rezagado p más en la autoregresión.
• N es el número total de observaciones.
• Podemos dividir la fórmula en dos partes: parte izquierda y parte derecha.

La parte de la izquierda:

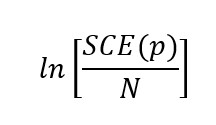
Representa la suma de los cuadrados de los residuos (SCE) de la autorregresión de p periodos rezagados, dividida entre el número total de observaciones (N).

Para hacer una estimación de los coeficientes empleamos mínimos cuadrados ordinarios (MCO). Entonces, cuando incluimos nuevos periodos rezagados, la SCE(p) solo puede mantenerse o decrecer.

Entonces, el incremento de un período rezagado en la autorregresión provoca:

• SCE(p): decrece o se mantiene constante. 
• Coeficiente de determinación: incrementa. 
• EFECTO TOTAL: un aumento de un período rezagado provoca una disminución en la parte izquierda de la fórmula.  

Ahora la parte derecha:

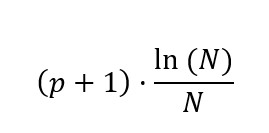
(p+1) representa el número total de coeficientes en la autorregresión, es decir, los regresores con sus periodos rezagados (p) y el intercepto (1).

Entonces, el incremento de un período rezagado en la autorregresión provoca:

• (p+1): aumenta porque incorporamos un período rezagado. 
• EFECTO TOTAL: un aumento de un período rezagado provoca un aumento en la parte derecha de la fórmula.  

Suponemos que queremos hacer una predicción sobre los precios de los forfaits para la siguiente temporada 2020 con una muestra de 5 años pero no sabemos cuántos periodos rezagados utilizar: ¿AR(2) o AR(3)?

• Descargamos los datos y calculamos los logaritmos naturales de los precios de los forfaits.

1. Estimamos los coeficientes mediante MCO y obtenemos:

Suma de los cuadrados de los residuos (SCE) para AR(2) = 0,011753112

Coeficiente de determinación para AR(2)= 0,085

2. Añadimos 1 período rezagado más para ver como cambia la SCE:

Suma de los cuadrados de los residuos para AR(3) = 0,006805295

Coeficiente de determinación para AR(3)= 0,47

Podemos ver que cuando añadimos un período rezagado en la autorregresión, el coeficiente de determinación aumenta y la SCE decrece en este caso.

• Calculamos el criterio de información bayesiano:

Cuanto más pequeño es el modelo BIC, más preferido será el modelo. Entonces, AR(3) sería el modelo preferido respecto AR(2) dado que su coeficiente de determinación es mayor, la SCE es menor y el modelo de Schwarz o criterio de información bayesiano también es menor.