Contraste de White
El contraste de White para heterocedasticidad implica regresar los residuos cuadráticos de Mínimos Cuadrados Ordinarios (MCO) sobre los valores ajustados de MCO y sobre los cuadrados de los valores ajustados.
Generalizando, los residuos cuadráticos de MCO se regresan sobre las variables explicativas. El objetivo principal de White es probar las formas de heterocedasticidad que invalidan los errores estándar típicos de MCO y sus correspondientes estadísticos.
Dicho de otro modo, el contraste de White nos permite comprobar la presencia de heterocedasticidad (el error, u, condicional sobre las variables explicativas varía en la población). Este contraste unifica en una sola ecuación los cuadrados y los productos cruzados de todas las variables independientes de la regresión. Dados los supuestos de Gauss-Markov, nos centramos en el supuesto de homocedasticidad siendo:
Var (u | x1,…,xk) = σ2
Un ejemplo de heterocedasticidad sería que en una ecuación sobre el cambio climático, la varianza de los factores no observados que afectan al cambio climático (factores que están dentro del error y E(u | x1,…,xk) ≠ σ2 ) aumenta con las emisiones de CO2 (Var (u | x1,…,xk) ≠ σ2 ). Aplicando el contraste de White estaríamos probando si Var (u | x1,…,xk) ≠ σ2 (heterocedasticidad) o Var (u | x1,…,xk) = σ2 (homocedasticidad). En este caso, rechazaríamos Var (u | x1,…,xk) = σ2 porque la varianza del error aumenta con las emisiones de CO2 y, por tanto, σ2 no es constante para toda la población.
Procedimiento
1. Partimos de una regresión lineal múltiple poblacional con k=2. Definimos (k) como el número de regresores.
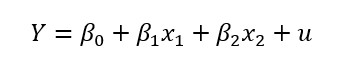
Suponemos cumplimiento de Gauss-Markov para que la estimación de MCO sea insesgada y consistente. En particular nos centramos en:
- E(u | x1,…,xk) = 0
- Var (u | x1,…,xk) = σ2
2. La hipótesis nula se basa en el cumplimiento de homocedasticidad.
H0: Var (u | x1,…,xk) = σ2
Para contrastar la H0 (homocedasticidad) se prueba si u2 está relacionada con una o más variables explicativas. De manera equivalente, la H0 puede expresarse como:
H0 : E( u2 | x1,…,xk) = E( u2 ) = σ2
3. Hacemos la estimación de MCO sobre el Modelo 1, donde la estimación de û2 es el cuadrado del error del Modelo 1. Construimos la ecuación û2 :
- Las variables independientes (xi).
- Los cuadrados de las variables independientes (xi2).
- Los productos cruzados (xi xh ∀ i ≠ h).
- Sustituimos B0 y Bk por δ0 y δk respectivamente.
- Sustituimos por u por v
Resultando en:
û2 = δ0 + δ1x1 + δ2x2 + δ3x12 + δ4x22 + δ5x1 x2 + v
Este error (v) tiene media cero con las variables independientes ( xi ) .
4. Planteamos las hipótesis a partir de la ecuación anterior:
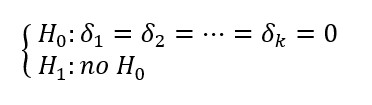
5. Utilizamos el estadístico F para calcular el nivel de significación conjunta de (x1,…,xk).
Recordamos como (k) el número de regresores en û2 .
6. Regla de rechazo:
- Valor-p < Fk,n-k-1 : rechazamos H0 = rechazamos presencia de homocedasticidad.
- Valor-p > Fk,n-k-1 : no tenemos suficientes evidencias significativas para rechazar H0 = no rechazamos presencia de homocedasticidad.
