Ángulo suplementario
El ángulo suplementario es aquel con el que se forma un ángulo llano. Es decir, dos ángulos son suplementarios si su sumatoria es 180º (grados sexagesimales) o π radianes.
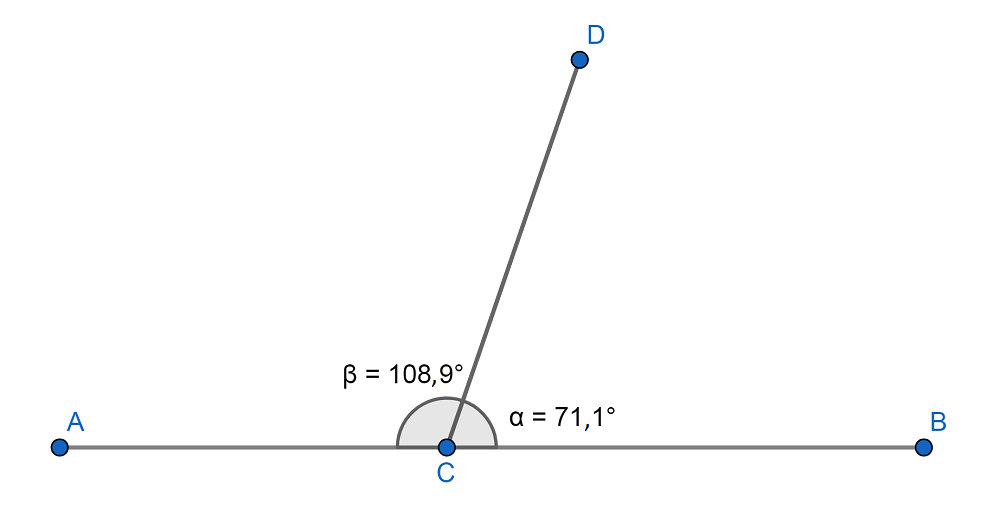
En el gráfico inferior, α y β son ángulos suplementarios (108,9º+71,1º=180º).
Para hallar el ángulo suplementario de un ángulo que mide xº solo calculamos la diferencia de 180º menos xº. Asimismo, si la medida del ángulo fuera en radianes restaríamos π – x (todo en radianes).
El ángulo suplementario es una las clasificaciones de los ángulos según el resultado de su suma con otro ángulo.
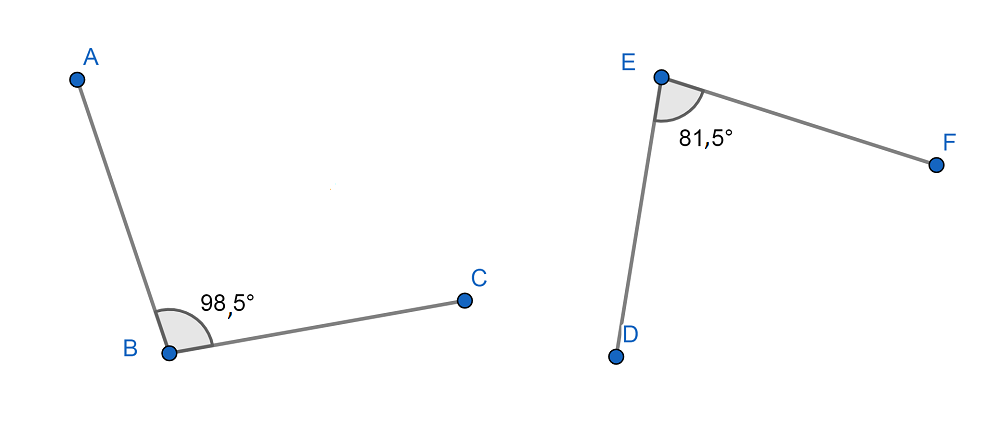
Vale precisar que dos ángulos suplementarios pueden ser consecutivos (como en la imagen de arriba), pero este no siempre es el caso. En la imagen inferior vemos dos ángulos suplementarios no consecutivos (98,5º+81,5º=180º).
Cabe recordar además que un ángulo es un arco formado por la intersección de dos rectas, semirrectas o segmentos.
Ejemplos de ángulo suplementario
Veamos algunos ejemplos de ángulo suplementario. Por ejemplo, si el ángulo x mide 130º, su ángulo suplementario mide 50º (180º-130º).
Asimismo, dos ángulos rectos o que miden 90º son suplementarios entre sí, y un ángulo mayor de 180º. Por ejemplo, uno que mide 230º, no tiene ángulo suplementario.
Otro punto adicional para observar es que un ángulo suplementario siempre mide menos de 180º. Es decir, no puede ser un ángulo cóncavo (mayor a 180º).
Asimismo, vale notar que dos ángulos agudos (menores de 90º) no pueden ser suplementarios.
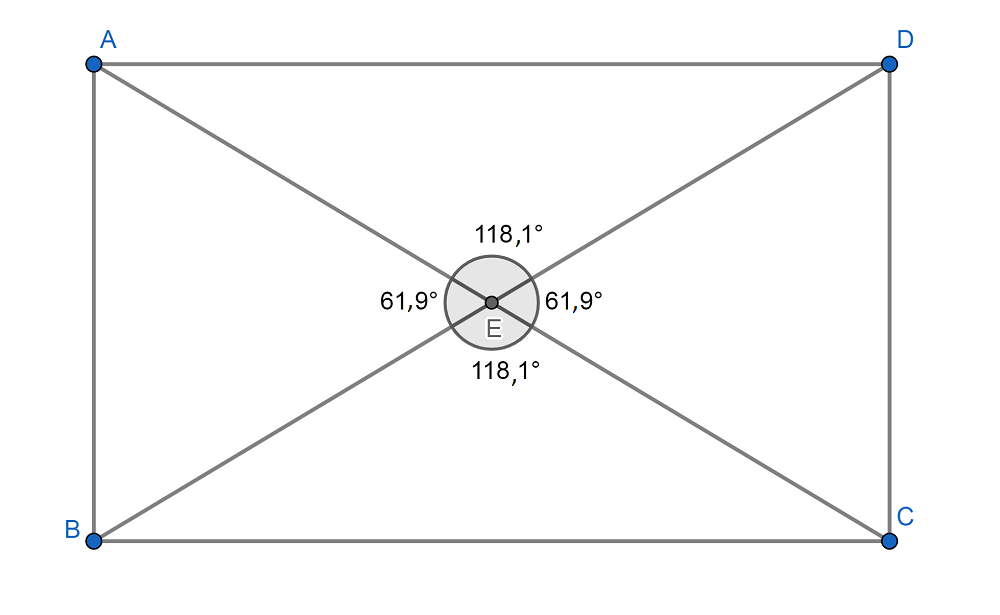
Para referirnos a un ejemplo más gráfico, si trazamos las dos diagonales de un cuadrilátero, por ejemplo, un rectángulo, en la intersección, aquellos ángulos adyacentes son suplementarios. Así, vemos en la imagen de abajo que se cumple que 118,1º+61,9=180º.
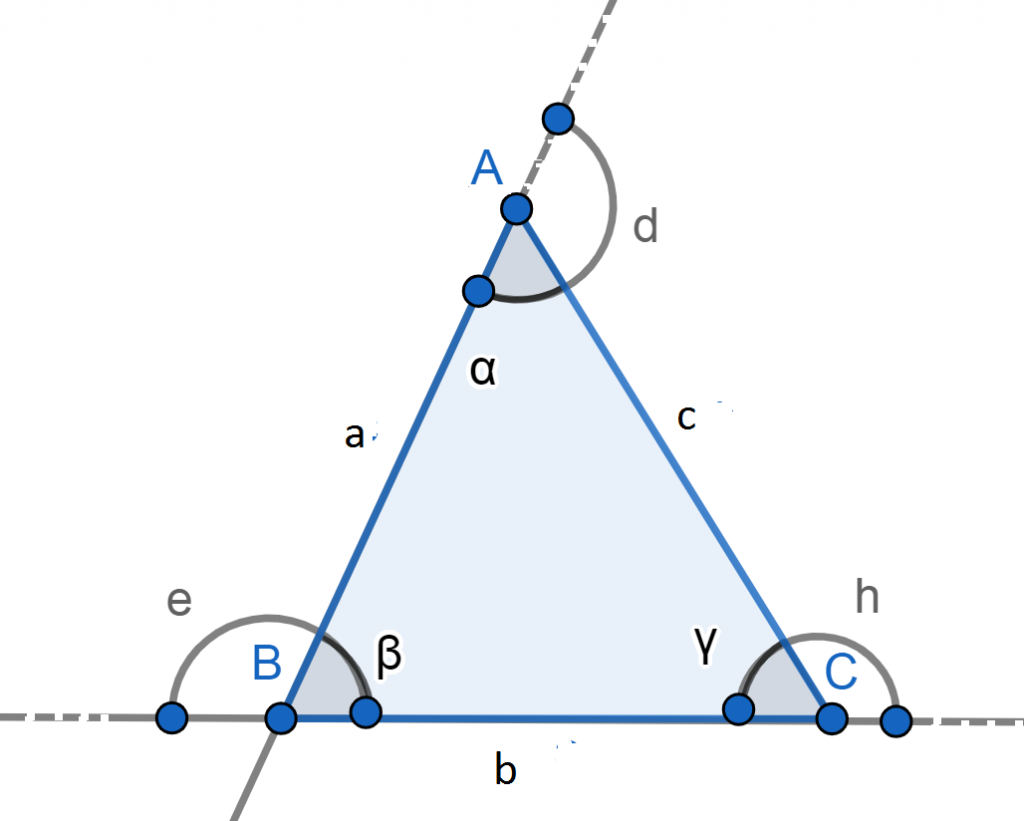
De igual modo, otro caso particular es el de los triángulos donde cada ángulo interior es suplementario a su correspondiente ángulo exterior del mismo vértice. Por ejemplo, en la imagen de abajo se cumple que:
180º= ∝+d= β+e= h+γ