Análisis de Fourier

Es decir, según el análisis de Fourier, se puede expresar una función periódica como la suma infinita de dos funciones trigonométricas: seno y coseno. Esto, eligiendo los argumentos adecuados para dichas funciones.

En este punto, debemos explicar que una función periódica es aquella que se comporta de forma secuencial, es decir, donde se repite un ciclo de manera repetitiva. A este ciclo que se repite se le denomina periodo.

Para observarlo de manera gráfica, imaginemos que tenemos una serie de ondas que se repiten una tras otra, como la frecuencia de un monitor cardíaco.

Entonces, estamos frente a un movimiento ondulatorio. Si recordamos los componentes de una onda, tenemos:

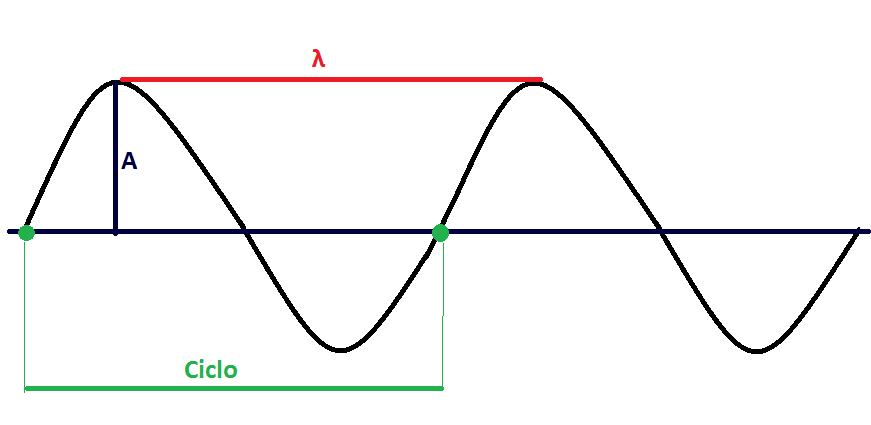
• Amplitud(A): Es la altura máxima de la onda.
• Longitud(λ): Es la distancia entre dos puntos máximos de una onda.
• Ciclo: Es el recorrido desde el inicio de una vibración hasta que se retorna al punto inicial.
• Periodo(T): Es el tiempo en el que se realiza una oscilación o ciclo.
• Frecuencia(f): Número de oscilaciones o ciclos por segundo o unidad de tiempo. Se corresponde con el periodo de la siguiente manera: f=1/T.

Una vez con estos conceptos claros, es más sencillo entender la composición del análisis de Fourier.

Como habíamos mencionado previamente, esta herramienta se utiliza en el caso de funciones periódicas, es decir, los ciclos serán repetitivos.

La serie que nos plantea el análisis de Fourier es el siguiente:

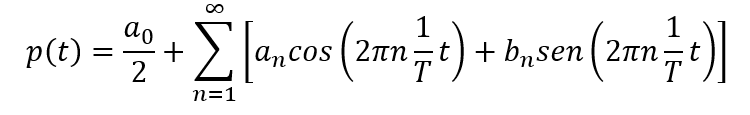
Para entender intuitivamente esta serie, vale explicar que p(t) es una función periódica donde t es la variable independiente.

Asimismo, dentro de la sumatoria, el argumento de la función seno y coseno es compuesto por 2π*(1/T)t, donde (1/T), como mencionamos anteriormente (cuando vimos los componentes de una onda), es la frecuencia.

Por lo tanto, si el argumento del seno o el coseno fuera 2π*4t, eso quiere decir que la frecuencia es 4. Y, por ende, el periodo, que es lo inverso de la frecuencia (f=1/T), es igual a 1/4.

De lo anterior, puedo interpretar que cada ciclo que se repite tiene una duración de 1/4 (1/4 de hora, por ejemplo).

Ahora, desde el punto de vista matemático, podemos deducir que los argumentos del seno y del coseno son múltiplos de la frecuencia de la función periódica.

Asimismo, a_n y b_n son los coeficientes de Fourier y son constantes, al igual que a_o.

Lo que estoy intentando demostrar con la serie de Fourier es que, sumando las ondas, que son las sumatorias de los senos y los cosenos, me aproximaré a la función que observamos en la imagen de arriba que está formada por segmentos rectos azules.

Lo que hemos realizado en este artículo es una definición muy intuitiva del análisis y de la serie de Fourier. Sin embargo, la demostración matemática es mucho más compleja. Lo que hemos buscado con en este artículo es animarte a investigar más sobre este tema, presentando una explicación trabajada por un no especialista (quien está escribiendo no es un matemático, sino un economista).