Definición de simetría axial
 Simetría, un concepto que deriva del latín symmetrĭa, hace referencia a la correspondencia que se registra entre la posición, la forma y el tamaño de los componentes de un todo. Axial, por su parte, es aquello vinculado a un eje (la pieza que actúa como sostén de algo y que, en ciertos contextos, permite que un determinado objeto gire).
Simetría, un concepto que deriva del latín symmetrĭa, hace referencia a la correspondencia que se registra entre la posición, la forma y el tamaño de los componentes de un todo. Axial, por su parte, es aquello vinculado a un eje (la pieza que actúa como sostén de algo y que, en ciertos contextos, permite que un determinado objeto gire).
Se conoce como simetría axial a la simetría que existe en torno a un eje cuando la totalidad de los semiplanos que se toman desde una determinada mediatriz exhiben las mismas características.
Para determinar si existe la simetría axial, se considera que los puntos que pertenecen a una figura sean coincidentes con los puntos que forman parte de otra figura, tomando a modo de referencia el eje de simetría (una línea). De esta manera, la simetría axial supone un fenómeno similar al que ocurre cuando un espejo refleja una imagen.
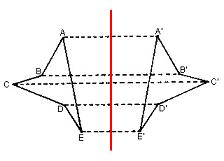
Con la simetría axial, las figuras simétricas disponen de puntos homólogos: el punto A de una figura es homólogo al punto A’ de la otra figura; el punto B de una figura es homólogo al punto B’ de la otra figura; etc. La distancia que existe entre los diferentes puntos que pertenecen a la figura original, por otra parte, resulta idéntica a la distancia existente entre los puntos que se hallan en la figura simétrica en cuestión.
Es importante mencionar que el concepto de simetría axial resulta útil en el terreno de la física. Cuando se parte de datos con simetría axial, la solución para determinadas incógnitas también cuenta con simetría axial, una particularidad que posibilita la reducción de las variables del problema.
¿Cómo dibujar la simetría axial de un polígono?
 Si bien la teoría fundamental de la simetría axial no resulta especialmente compleja, siempre es conveniente llevar los conocimientos a la práctica, para poder interiorizarlos de forma más efectiva. En este caso en particular, tenemos la ventaja de su compatibilidad con el dibujo, algo que la mayoría de las personas podemos realizar con una cierta facilidad. Por ello, veremos a continuación una serie de pasos para obtener una figura simétrica a otra.
Si bien la teoría fundamental de la simetría axial no resulta especialmente compleja, siempre es conveniente llevar los conocimientos a la práctica, para poder interiorizarlos de forma más efectiva. En este caso en particular, tenemos la ventaja de su compatibilidad con el dibujo, algo que la mayoría de las personas podemos realizar con una cierta facilidad. Por ello, veremos a continuación una serie de pasos para obtener una figura simétrica a otra.
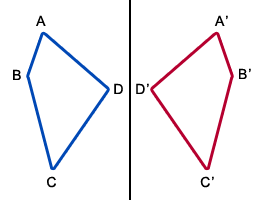
En primer lugar es necesario dibujar una figura y determinar los puntos que la componen. Para este ejemplo nos basaremos en un polígono de cuatro vértices (A, B, C y D), aunque los pasos funcionan para cualquier otro caso. Habiendo trazado el polígono y definido adecuadamente sus vértices, llega el paso más importante: establecer la posición y la orientación del eje de simetría.
Aunque en los ejemplos más sencillos estamos acostumbrados a ver ejes de simetría axial perpendiculares al suelo, que nos ofrezcan una figura al lado de la otra, es necesario resaltar que el ángulo de dicho eje es indiferente. Para entender esto, podemos pensar en que el eje es un espejo que deseamos utilizar para reflejar un objeto: no importa si lo ubicamos delante, detrás o a un costado del mismo, así como tampoco si lo giramos, ya que siempre hará su trabajo con éxito. De hecho, el eje puede pasar por uno de los puntos de la figura original, si quisiéramos un resultado en el cual ambas se tocaran.
Una vez que hayamos dibujado el eje de simetría axial, podemos comenzar a trazar los puntos de la nueva figura. Para ello, debemos medir la distancia de cada uno de los vértices originales y el eje, a través de una línea perpendicular al mismo, y luego recorrer esa misma distancia hacia el otro lado del eje hasta dar con la posición homóloga. Dado que nuestra figura tiene tan sólo cuatro puntos, se trata de una tarea relativamente sencilla.
Teniendo los cuatro vértices homólogos, a los cuales llamaremos A’, B’, C’ y D’, sólo queda trazar cada uno de los lados correspondientes.
