Definición de resta de fracciones
El término resta suele hacer mención a la operación que consiste en restar. Este verbo, por su parte, se refiere a reducir, achicar o separar una parte de un todo. Si nos centramos en la matemática, restar consiste encontrar la diferencia que existe entre dos expresiones o cantidades.
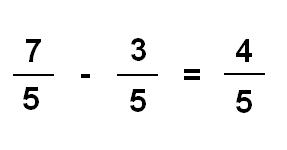 De este modo podemos hablar de diferentes tipos de resta, como la resta algebraica, la resta de polinomios, la resta de vectores y la resta de matrices. En esta oportunidad, nos vamos a centrar en la resta de fracciones.
De este modo podemos hablar de diferentes tipos de resta, como la resta algebraica, la resta de polinomios, la resta de vectores y la resta de matrices. En esta oportunidad, nos vamos a centrar en la resta de fracciones.
Para comprender esta operación, debemos saber que, en matemática, una fracción es una expresión que revela una división. Se trata, en otras palabras, de una cantidad que está dividida entre otra cantidad.
Una fracción está formada por dos números: el superior se denomina numerador, mientras que el inferior se conoce como denominador. La manera de desarrollar una resta de fracciones dependerá de si ambas fracciones tienen el mismo denominador o no.
Cuando las fracciones tienen el mismo denominador, simplemente debemos restar los numeradores como en cualquier resta algebraica y mantener el denominador. Por ejemplo:
7/2 – 4/2 = (7 – 4)/2 = 3/2
Si los denominadores son distintos, primero debemos igualarlos, hallando el denominador común. Para hacer esto podemos multiplicar cada fracción por el denominador de la otra:
9/7 – 2/3
(9 x 3) / (7 x 3) – (2 x 7) / (3 x 7)
27/21 – 14/21
Una vez que hallamos un denominador común, procedemos a restar como explicamos en el ejemplo anterior:
(27 – 14)/21 = 13/21
Los estudiantes en la etapa infantil, antes de entrar en la Secundaria, es cuando comienzan a aprender a sumar y restar fracciones, ya que estas operaciones matemáticas son básicas y fundamentales a la hora de que puedan ir ampliando sus conocimientos en dicha asignatura.
En concreto, comienzan realizando problemas con dos fracciones y luego, para afianzar lo que han aprendido y coger soltura al respecto, procederán a realizar la misma operación pero con tres o más. En ese caso, el procedimiento es similar. Así, en el caso de que compartan denominador todo es mucho más sencillo porque sólo tendrán que proceder a restar los numeradores.
Si lo que sucede es que tienen un denominador diferente, pues habrá que seguir el proceso anteriormente citado de encontrar lo que es el mínimo común múltiplo y a partir de este, una vez que se haya logrado, desarrollar lo que sería la resta con los numeradores.
La suma y la resta son las operaciones más sencillas de acometer con las mencionadas fracciones. No obstante, no hay que pasar por alto que también se puede optar por realizar multiplicaciones y divisiones. En el primer caso, lo que hay que hacer es multiplicar los numeradores por un lado y los denominadores por otro. Ejemplo: 3/2 x 5/4= (3 x 5) / (2 x 4) = 15/8
En el segundo caso, en el de dividir dos fracciones, lo que hay que hacer es multiplicar el numerador de una fracción por el denominador de la otra para obtener el numerador final y multiplicar el denominador de la primera fracción por el numerador de la segunda conseguir el denominador final. Ejemplo: 3/2 : 5/4 = (3 x 4) : (2 x 5) = 12/10.
