Definición de punto de aplicación
Punto es un término con múltiples acepciones. Puede tratarse de una mancha circular, un signo ortográfico, una unidad para llevar el registro de un tanteador o incluso un lugar. Aplicación, por su parte, es el proceso y el efecto de aplicar (poner algo en práctica, adjudicarlo).
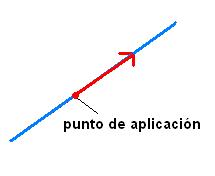 El concepto de punto de aplicación se utiliza para nombrar al sitio determinando en el cual se aplica una fuerza. Se trata de un lugar geométrico, vinculado a un vector.
El concepto de punto de aplicación se utiliza para nombrar al sitio determinando en el cual se aplica una fuerza. Se trata de un lugar geométrico, vinculado a un vector.
Para comprender con precisión qué es el punto de aplicación, debemos tener conocimientos sobre varias nociones. Primero hay que saber que una fuerza es aquello que permite el desplazamiento o la deformación de un cuerpo. La fuerza, por lo tanto, altera al estado de un objeto.
La representación gráfica de las fuerzas se realiza a través de vectores, que son segmentos con un extremo con forma de flecha, indicando la dirección y el sentido de la fuerza.
Al igual que es importante el punto de aplicación, la dirección y el sentido como parte fundamental de un vector, no hay que olvidar tampoco que hay otro elemento igualmente significativo. Nos estamos refiriendo a la magnitud. Esta viene a ser el tamaño que tiene el citado vector en base a la escala que se esté empleando en ese momento.
Retomando, por lo tanto, la idea de punto de aplicación, podemos decir que éste es el lugar en el cual se aplica la fuerza y donde, por lo tanto, se origina el vector.
Hay que saber que sobre un cuerpo suelen actuar, por regla general, dos o más fuerzas dando forma a lo que se conoce como sistemas de fuerzas. Estos, que luego acaban siendo una fuerza llamada resultante, se pueden clasificar en varios grupos siendo los más significativos los siguientes:
-Concurrentes, que se caracterizan porque las líneas de acción llegan a converger en un único punto, que da lugar a la existencia de ángulos.
-Colineales, que son las fuerzas o sistemas de fuerzas que proceden a actuar en una única y misma dirección.
-Paralelas. Como su propio nombre indica se trata del sistema en el que las fuerzas llevan una dirección que es paralela unas a las otras.
Es importante aclarar que, en el campo de la física, se suele trabajar con vectores que tienen independencia respecto a su punto de aplicación. Estos vectores, definidos como equipolentes, pueden desplazarse por distintas zonas del espacio geométrico sin sufrir cambios mientras se mantenga la longitud (conocida como módulo), el sentido (hacia donde apunta) y la dirección (la recta sobre la que se dibuja el vector).
Hay que exponer que, en ocasiones, muchas personas suelen confundir lo que es punto de aplicación con sentido de la fuerza. En ese caso, deben tener claro qué es una cosa y qué es la otra. De esta manera, se puede decir que el primer término hace referencia al lugar donde la fuerza entra en contacto directo con el cuerpo en cuestión. Por otro lado, el sentido es la dirección que toma esa fuerza y se representa mediante una flecha.
