Definición de proporción áurea
La proporción áurea es un número irracional que descubrieron pensadores de la Antigüedad al advertir el vínculo existente entre dos segmentos pertenecientes a una misma recta. Dicha proporción puede hallarse en la naturaleza (flores, hojas, etc.) y en figuras geométricas y se le otorga una condición estética: aquello cuyas formas respetan la proporción áurea es considerado bello.
Esta proporción, que también suele mencionarse como razón áurea, número áureo o divina proporción, incluso solía ser señalada por sus supuestas propiedades místicas. Su ecuación se expresa como 1 más la raíz cuadrada de 5, todo sobre 2, y el resultado es aproximadamente igual a 1,61803398874989…

A la proporción áurea también se la conoce como divina proporción, número áureo o razón áurea.
Una relación entre dos segmentos
Puede decirse que la proporción áurea surge de la relación entre un segmento a y un segmento b. El segmento a es más extenso que el segmento b, mientras que la longitud total de la recta es, al segmento a, como el segmento a es al segmento b.
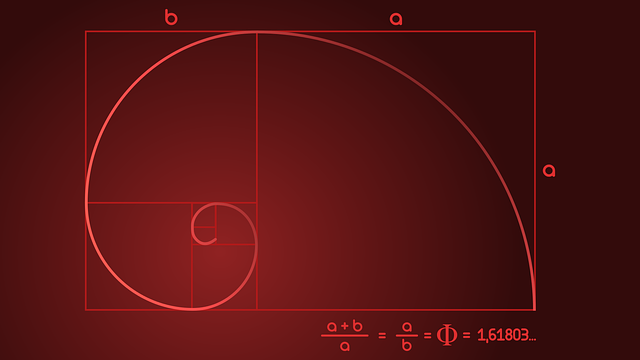
Si ponemos la proporción áurea en una expresión algebraica, obtenemos la siguiente ecuación: (a + b) / a = a / b. El número áureo, que se lo menciona con la letra griega phi, es el resultado de la división entre a y b.
Otra manera de entender la noción de proporción áurea consiste en hallar la siguiente equivalencia, reflejada también en la expresión algebraica anterior: si tomamos un segmento y lo cortamos en dos, el cociente de la división de la longitud de la recta (a+b) y la longitud del segmento más largo (a) debe ser idéntico al cociente de la división de la longitud del segmento más largo (a) y la longitud del segmento menor (b).
La sucesión de Fibonacci es una secuencia infinita de números.
Proporción áurea y sucesión de Fibonacci
Un concepto íntimamente ligado al de proporción áurea es la sucesión de Fibonacci, descubierta por el matemático italiano Leonardo de Pisa, también responsable de la difusión del sistema árabe de numeración en el continente europeo. Dicha sucesión presenta una secuencia infinita de números en la cual la suma de cualquier par da como resultado el número siguiente (0, 1, 1, 2, 3, 5, 8, 13, etcétera). Curiosamente, si dividimos cualquier número de la sucesión de Fibonacci por el que lo precede (especialmente a partir del 5) nos da un resultado que se aproxima al número áureo.
Aunque su definición resulte abstracta y algo difícil de entender, la aplicación de la proporción áurea es importante en la fotografía, la pintura, la escultura y otras artes que suelen vincular el ideal de belleza a las simetrías y las proporciones.
La Espiral de Oro
La representación gráfica de la proporción áurea, que se obtiene trazando una serie de rectángulos y uniendo algunos de sus vértices con una línea espiralada, da como resultado la conocida Espiral de Oro, la cual se encuentra muy frecuentemente en la naturaleza (dos ejemplos son las conchas marinas y las semillas de girasol). En la fotografía, el uso de dicha figura para ubicar los diferentes objetos puede ofrecer resultados impresionantes, con una armonía y una fluidez que reflejan el espíritu de la escena.
A pesar de los beneficios que puede traer la proporción áurea a la fotografía, los expertos recomiendan usar este concepto como una guía, en lugar de convertirlo en una estructura rígida que impida la composición espontánea y creativa de las imágenes. Además, es importante resaltar que no todas las cámaras tienen las características adecuadas para su aplicación (por ejemplo, por contar con sensores cuadrados, ya que la espiral completa abarca un rectángulo, o sea que es más ancha que alta), y eso no significa que no sean capaces de realizar buenas capturas.
Del mismo modo, la aplicación de la Espiral de Oro en la pintura y la escultura puede elevar los resultados, pero de ninguna manera debería convertirse en el único camino hacia la creación de obras artísticas.
