Definición de progresión geométrica
La noción de progresión puede asociarse a una sucesión, un progreso, un desarrollo o un avance de algo. Geométrico, por su parte, es un adjetivo vinculado a la geometría (la rama de la matemática orientada al análisis de las características de las figuras en un espacio o en un plano).
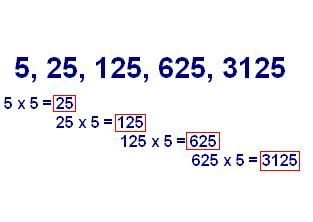 Estas definiciones nos ayudan a comprender a qué se refiere la idea de progresión geométrica. Se trata de una secuencia formada por elementos sucesivos, obtenidos mediante la multiplicación del elemento previo por un valor constante. Dicha constante recibe el nombre de factor o razón.
Estas definiciones nos ayudan a comprender a qué se refiere la idea de progresión geométrica. Se trata de una secuencia formada por elementos sucesivos, obtenidos mediante la multiplicación del elemento previo por un valor constante. Dicha constante recibe el nombre de factor o razón.
Lo habitual es que una progresión geométrica refiera a una secuencia que dispone de un número finito de términos. En cambio, si la secuencia se extiende hasta el infinito, suele hablarse de sucesión geométrica.
Una progresión geométrica cuya razón sea 5 sería la siguiente: 5, 25, 125, 625, 3125, 15625. Como puede apreciarse, dicha progresión se obtiene multiplicando cada término por 5: 5 x 5 = 25; 25 x 5 = 125; 125 x 5 = 625; 625 x 5 = 3125; 3125 x 5= 15625.
Dentro del ámbito de la citada progresión geométrica, tenemos que exponer que existe lo que se da en llamar interpolación de términos. Este se usa para definir lo que es la construcción de una progresión geométrica que se identifique por el hecho de que sus extremos tenga números dados. Así, por ejemplo, se establece que hay que interpolar tres números entre el 3 y el 48 el resultado estará conformado por el 6, el 12 y el 24.
¿Cómo se puede calcular esa interpolación? Básicamente llevando a cabo la siguiente fórmula:
r = m+1 √b/a
En esa fórmula, m corresponde al número de medios que hay que interpolar y tanto b como a son los números que se sitúan en los extremos. Así, en el ejemplo dado anteriormente, m sería el número 3, b sería 48 y a sería el 3.
De la misma manera, no podemos pasar por alto que se pueden llevar a cabo otra serie de operaciones matemáticas con lo que es cualquier progresión geométrica. En concreto, se puede proceder a la suma de un número determinado de los términos consecutivos en una citada progresión cualquiera, y también incluso si esta es decreciente.
Es interesante saber en este sentido que la suma de los términos de la progresión es igual al último término por la razón menos el primer término dividido por la razón menos 1.
Pero hay aún hay más. También se puede realizar el producto de un determinado número de términos equidistantes de una progresión geométrica.
Es importante tener en cuenta que el factor constante de una progresión geométrica puede un número negativo o incluso un número fraccionario. Cuando la razón es un número negativo, los elementos de la progresión geométrica alternarán entre valores positivos y negativos:
Progresión geométrica con factor -3: 8; -24; 72; -216.
Progresión geométrica con factor 1,5: 2; 3; 4,5; 6,75.
Cabe destacar, por último, que si el factor es 1, la progresión geométrica será constante:
Progresión geométrica con factor 1: 5, 5, 5, 5, 5 (ya que 5 x 1 = 5; 5 x 1 = 5, etc.)
