Definición de producto escalar
En el terreno de las matemáticas, se denomina producto al resultado de una multiplicación. La idea de escalar, en tanto, puede emplearse para nombrar al número que posibilita la descripción de un fenómeno con magnitud, aunque dejando de lado la dirección del vector.
 Es importante considerar antes de avanzar que un vector es una magnitud que exige la consideración, además de su cuantía, de su sentido, dirección y punto de aplicación.
Es importante considerar antes de avanzar que un vector es una magnitud que exige la consideración, además de su cuantía, de su sentido, dirección y punto de aplicación.
Se conoce como producto escalar, en este marco, a la operación del álgebra que parte de dos secuencias numéricas con la misma longitud (que suelen tener la forma de vectores) y arriba a un único número.
También llamado producto punto, producto interior o producto interno, el producto escalar se obtiene al sumar los productos de las entradas de un par de secuencias numéricas. El resultado no es un vector, sino un escalar.
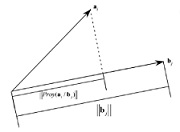
Puede afirmarse que el producto escalar de un vector a→ y un vector b→ (a→ ⋅ b→) arroja como resultado un número (el escalar) tal que a→ ⋅ b→ = (a→) ⋅ (b→) ⋅ cos(α), siendo α el ángulo que componen los dos vectores (a→ y b→).
Esto nos permite sostener que, para la geometría, el producto escalar es la multiplicación de las magnitudes euclidianas de dos vectores y el coseno del ángulo que forman ambos.
Si los vectores son paralelos y comparten el mismo sentido, el producto escalar equivale a la multiplicación de los módulos. En cambio, si el sentido es diferente, se obtiene multiplicando sus módulos pero agregando el signo negativo.
En el caso de los vectores perpendiculares, el ángulo formado es de 90º y el producto escalar resulta igual a 0.
