Definición de momento de inercia
 La noción de momento de inercia se usa en el ámbito de la física. Para comprender a qué alude la expresión, primero es importante entender los términos que la conforman.
La noción de momento de inercia se usa en el ámbito de la física. Para comprender a qué alude la expresión, primero es importante entender los términos que la conforman.
En el terreno específico de la física, momento refiere a la cantidad de movimiento: se trata de la magnitud resultante de la multiplicación de la masa de un cuerpo por su velocidad. La inercia, en tanto, es la propiedad de un objeto de conservar su estado de movimiento o reposo a menos que actúe una fuerza sobre él.
Según indica el diccionario de la Real Academia Española (RAE), el momento de inercia es la sumatoria de los productos que se obtienen al multiplicar la masa de los distintos elementos de un cuerpo por el cuadrado de la distancia hacia su eje de rotación.
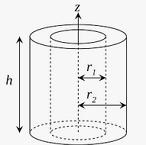
Dicho de otro modo, el momento de inercia está vinculado a cómo se distribuye la masa del cuerpo respecto a un cierto eje de giro. Se determina, de esta manera, de acuerdo a la geometría corporal y a la posición del eje, más allá de las fuerzas que producen el movimiento.
Es importante señalar que la inercia puede entenderse como la resistencia ejercida por el cuerpo a una alteración del movimiento. El momento de inercia, en este marco, resulta análogo al momento de la masa inercial ante un movimiento uniforme y rectilíneo.
Un cuerpo puede contar con distintos ejes de rotación, repartidos en diferentes zonas de su estructura. Por eso un mismo objeto tiene la posibilidad de tener varios momentos de inercia.
Es importante entender que los ejes de rotación que suelen usarse o tomarse como referencia en el terreno de la física son imaginarios, aunque puede darse el caso de que coincidan con objetos materiales que actúen de esta manera. Cuando rotamos las diferentes partes de nuestro cuerpo, por ejemplo, no existen huesos cilíndricos alrededor de los cuales hagamos estos movimientos, sino más bien restricciones musculares que las van guiando.
Los ejes de rotación son, por lo tanto, recursos imaginarios que se usan en el campo de la física para entender estos movimientos y poder hacer cálculos relacionados con ellos, tanto para estudiar cada aspecto de ellos como para anticiparlos o provocarlos.
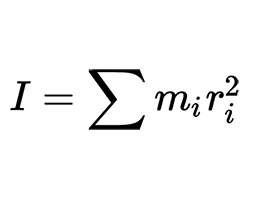 Con respecto a la ecuación que se usa para expresar el momento de inercia, podemos decir que existen varias, cada una con diferentes propósitos. Si tomamos un ejemplo de la definición básica, enunciada en un párrafo anterior, la notación matemática de la misma se encuentra en la imagen de la derecha.
Con respecto a la ecuación que se usa para expresar el momento de inercia, podemos decir que existen varias, cada una con diferentes propósitos. Si tomamos un ejemplo de la definición básica, enunciada en un párrafo anterior, la notación matemática de la misma se encuentra en la imagen de la derecha.
Aquí nos encontramos con las variables: I, que representa el momento de inercia mismo; m, las masas de las partículas; r, la distancia mínima entre el eje y cada partícula. El símbolo Σ, por otro lado, es el que se denomina sumatorio, aunque también se puede usar en femenino, sumatoria. Se trata de una notación usada para denotar la suma de una sucesión de términos que se encuentran delimitados de forma expresa.
Otro nombre por el que se conoce el sumatorio es notación sigma, precisamente porque usa la decimoctava letra griega llamada de esta manera. Si bien se trata de una suma, no debemos usar estos términos de forma indistinta, ya que el sumatorio tiene reglas bien definidas. Mientras que la suma es una operación que puede relacionar cualquier grupo de números, en cualquier cantidad, el sumatorio debe respetar un valor inicial i (su límite inferior) y un valor final n (su límite superior>, respetando que i sea menor o igual a n.
En la ecuación del momento de inercia no deben expresarse los límites porque el sumatorio incluye todos los elementos, es decir, las masas de todas las partículas del sistema.
