Definición de mínimo común múltiplo
 Mínimo común múltiplo (MCM) es un concepto que se utiliza en la matemática. El MCM entre varios números naturales es el número natural más pequeño que es distinto de 0 y que resulta múltiplo de cada uno de ellos.
Mínimo común múltiplo (MCM) es un concepto que se utiliza en la matemática. El MCM entre varios números naturales es el número natural más pequeño que es distinto de 0 y que resulta múltiplo de cada uno de ellos.
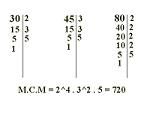
Para calcular el MCM de dos números, es necesario descomponerlos en factores primos. El MCM, por lo tanto, será la cifra que obtengamos a partir de la multiplicación de los factores no comunes y comunes con elevación a la mayor potencia. Veamos a continuación un ejemplo práctico para entender a fondo el procedimiento:
Si tomamos los números 32 y 50, el primer paso será comenzar a dividir cada uno por 2 hasta que sea imposible obtener un resultado entero, y entonces continuar por el 3, y así sucesivamente hasta que ya no se pueda seguir sin entrar en el terreno de los números reales. Comenzando por 32, podremos dividirlo por 2, obteniendo 16 y repetir esta operación hasta llegar al 1, habiendo realizado 5 divisiones, lo que nos indica (dicho de otra forma) que 32 es igual a elevar 2 a su quinta potencia.
El número restante es ligeramente más complicado, ya que deberemos cambiar de divisor; 50 dividido 2 nos da 25, que no es múltiplo de 2. Por lo tanto, será necesario buscar un divisor que nos devuelva un cociente sin resto, que en este caso es el número 5. Con él podremos continuar hasta obtener el resultado 1, y observando detenidamente los divisores, podremos expresar 50 como el producto de 2 por 5 al cuadrado. Éste es el momento de comparar los factores de ambas cifras (32 y 50) y confeccionar una fórmula en la que figuren todos los factores resultantes de ambas listas, elevados a la mayor potencia que hayamos obtenido. En otras palabras, el mínimo común múltiplo de 32 y 50 es igual a la multiplicación de 2 elevado a la quinta potencia por 5 al cuadrado, que da 800.
En algunos casos, obtener el MCM es muy sencillo. El primer paso es calcular los múltiplos de los números y luego buscar la primera equivalencia, yendo de menor a mayor (es decir, el número más pequeño que es múltiplo de los dos y que, por lo tanto, aparece en las dos listas de múltiplos que calculamos previamente).
Si queremos descubrir el MCM de 3 y 5, empezaremos confeccionando una lista de sus múltiplos:
3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55
Como puede apreciarse, el primer múltiplo común de 3 y 5 es 15. Otros múltiplos comunes de 3 y 5 son 30, 45 y 60, por ejemplo.
 El MCM puede utilizarse para la suma de fracciones de distinto denominador. Lo que debemos hacer es considerar el mínimo común múltiplo de los denominadores de las fracciones y, tras convertirlas en fracciones equivalentes, sumarlas. En otras palabras, supongamos que debemos sumar las fracciones 7/15 y 4/10; a simple vista se aprecia que sus denominadores son diferentes, por lo cual no es posible proceder a sumar sus numeradores. Para resolver dicha operación, tal y como se ha expresado anteriormente, será necesario en primer lugar volver compatibles ambas fracciones.
El MCM puede utilizarse para la suma de fracciones de distinto denominador. Lo que debemos hacer es considerar el mínimo común múltiplo de los denominadores de las fracciones y, tras convertirlas en fracciones equivalentes, sumarlas. En otras palabras, supongamos que debemos sumar las fracciones 7/15 y 4/10; a simple vista se aprecia que sus denominadores son diferentes, por lo cual no es posible proceder a sumar sus numeradores. Para resolver dicha operación, tal y como se ha expresado anteriormente, será necesario en primer lugar volver compatibles ambas fracciones.
Con ese objetivo, deberemos buscar el mínimo común múltiplo de sus denominadores, que en este caso es 30. Luego, para convertir sus numeradores, dividiremos este valor por cada denominador y multiplicaremos su cociente por el numerador: (30 / 15) * 7 = 14 y (30 / 10) * 4 = 12. Así, con las fracciones 14/30 y 12/30, sólo queda sumar sus numeradores, lo cual nos devuelve la fracción 26/30 (nótese que el denominador permanece intacto).
Otro uso del MCM se encuentra en el ámbito de las expresiones algebraicas. El MCM de dos de estas expresiones equivale a aquélla con el coeficiente numérico más pequeño y grado inferior que es susceptible de división por todas las expresiones dadas sin que quede resto.
