Definición de fracción impropia
Para poder conocer el significado del término fracción impropia se hace necesario, en primer lugar, descubrir el origen etimológico de las dos palabras que le dan forma:
-Fracción, en primer lugar, procede del latín. Exactamente deriva de “fractio, fractionis”, que puede traducirse como “pedazo roto” y que deriva al mismo tiempo del verbo “frangere”, que es sinónimo de “romper”.
-Impropia, en segundo lugar, tenemos que subrayar que también emana del latín. En su caso, de “impropius”, que puede traducirse como “que no pertenece a las características que corresponden a una persona o cosa”. Una palabra esa que es fruto de la suma de varios componentes léxicos, tales como los siguientes: el prefijo “in-”, que significa “no sin”; el vocablo “pro”, que es sinónimo de “a favor”; el adjetivo “privo”, que es equivalente a “privado”; y el sufijo “-io”, que se usa para indicar “resultado” o “efecto”.
Una fracción es una expresión que hace referencia a una división. Se compone de dos números separados por una línea divisora: el numerador (que se ubica sobre esta línea) es el número a ser dividido, mientras que el denominador (que aparece debajo de la línea) es la cantidad por la cual se divide.
Veamos un ejemplo. 5/8 es una fracción que tiene al número 5 como numerador y al número 8 como denominador. En este caso, la fracción indica la división de 5 en 8: 0,625.
Según sus características, podemos clasificar a las fracciones de distintas maneras. Una fracción impropia es aquella cuyo denominador es menor que su numerador. Por lo tanto, la fracción resulta mayor a 1. En cambio, cuando el denominador es mayor que el numerador, estamos ante una fracción propia, que representa un número mayor a 0 pero menor a 1.
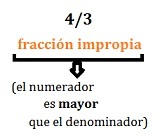
Teniendo en cuenta esta explicación, podemos afirmar que 4/3, por citar un caso, es una fracción impropia. Su numerador es 4 y su denominador, 3: como se puede advertir, el numerador es mayor que el denominador. Si resolvemos la división, notaremos que el resultado es mayor a 1: 1,33.
En ocasiones el numerador resulta mucho más grande que el denominador. Ese el caso de la fracción 5872/4. El numerador (5872) es 1468 veces mayor que el denominador (4), tal como descubrimos al realizar la división.
8/3, 54/7, 581/29, 892/431 y 182530/51779 son otras fracciones impropias. La condición es siempre la misma: que el numerador sea mayor que el denominador o, dicho de otro modo, que el denominador sea menor que el numerador. Cuando se cumple esta propiedad, la fracción recibe la denominación de impropia.
Además de todo lo indicado no podemos pasar por alto tampoco que las fracciones impropias tienen la particularidad de que pueden convertirse o representarse mediante un número mixto, es decir, como un número natural más una fracción propia.
Para poder conseguir representar a una fracción impropia de esa manera el proceso que hay que seguir es dividir el numerador entre el denominador. El cociente que quede será el número natural mientras que lo que es el resto será el numerador de la fracción propia.