Definición de colineales
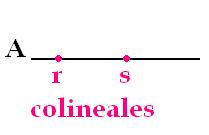 El adjetivo colineal se emplea en el terreno de la geometría para calificar al punto que está ubicado en la misma recta que otro punto. Supongamos que, en la recta A, es posible encontrar los puntos r, s y t. Estos tres puntos, por lo tanto, son colineales: se hallan en la misma recta.
El adjetivo colineal se emplea en el terreno de la geometría para calificar al punto que está ubicado en la misma recta que otro punto. Supongamos que, en la recta A, es posible encontrar los puntos r, s y t. Estos tres puntos, por lo tanto, son colineales: se hallan en la misma recta.
Para comprender con precisión a qué alude la idea de colineal, debemos definir términos como punto y recta. Los puntos son figuras geométricas que, sin volumen, área, longitud ni dimensión, permiten describir una cierta posición en el espacio, a partir de un sistema de coordenadas ya establecido. Una recta, por su parte, es una sucesión infinita de puntos que se desarrolla en una misma dirección.
Gráficamente, una recta es una línea que podría extenderse indefinidamente tanto hacia atrás como hacia delante, siempre en la misma dirección. Todos los puntos que están incluidos en dicha recta con colineales. Si dibujamos una recta B y en ella ubicamos los puntos k y l, ambos serán colineales.
En cambio, si en la recta A se encuentra el punto r y en la recta B se halla el punto k, estos dos puntos (r y k) no son colineales debido a que ambos pertenecen a rectas distintas.
Es muy importante resaltar que las rectas son imaginarias e infinitas, y de ninguna manera son segmentos que podamos trazar sobre una hoja o un muro, sino que éstos forman parte de ellas, en todo caso. Por ello, hablar de rectas y puntos no es tan sencillo ni determinante como hablar de objetos del mundo material, como ser un lápiz, que existe y no puede ser otro ni tampoco no ser visto.
Sin embargo, algo que comparten un lápiz y una recta es que el nombre que reciben es absolutamente arbitrario, tanto por cuestiones propias de la lengua usada para denominarlos como por la decisión del hablante a la hora de dirigirse a ellos: en cada idioma las palabras usadas para designarlos son diferentes, así como la fonética y, por qué no, la cantidad de términos necesarios, pero el lápiz y una recta dada siguen siendo los mismos.
 En el terreno de la geometría, podemos definir un plano de dos dimensiones por medio de una fórmula y luego identificar una de sus infinitas rectas con la letra R, para no faltar a las convenciones, pero para saber si dos o más puntos son colineales solamente importa que superen la comprobación matemática, independientemente del nombre que cada uno le dé a la recta o al plano.
En el terreno de la geometría, podemos definir un plano de dos dimensiones por medio de una fórmula y luego identificar una de sus infinitas rectas con la letra R, para no faltar a las convenciones, pero para saber si dos o más puntos son colineales solamente importa que superen la comprobación matemática, independientemente del nombre que cada uno le dé a la recta o al plano.
Cuando tenemos solamente dos puntos bidimensionales y deseamos saber si son colineales, podemos remitirnos a la ecuación de la recta en cuestión, escoger uno de sus puntos y comprobar si incluyéndolo en la fórmula nos da el restante como resultado. Para tres o más puntos, siempre podemos agruparlos de a dos y calcular sus distancias, para luego sumar los resultados y compararlos con la distancia que existe entre los más alejados: si es igual, entonces son todos colineales.
Los segmentos también pueden calificarse como colineales. Recordemos que un segmento es una porción de recta que se desarrolla entre dos puntos (denominados puntos extremos). Cuando dos segmentos comparten un punto extremo, son segmentos consecutivos. Entre ellos, los segmentos colineales son los que se ubican en una misma recta. Por el contrario, cuando los segmentos consecutivos se desarrollan en rectas diferentes se habla de segmentos no colineales.
Con respecto a las operaciones que podemos realizar con los segmentos colineales, si sumamos dos o más consecutivos colineales obtenemos uno que lo determinan los extremos no comunes del conjunto. Desde un punto de vista geométrico, esta operación nos da como resultado un nuevo segmento que puede construirse ordenando los originales de forma colineal hasta dar con uno cuyos extremos sean uno de cada punto del primero y el último.
