InicioGeografía

Plano cartesiano

Te explicamos qué es el plano cartesiano, cómo se creó, sus cuadrantes y elementos. Además, cómo se representan las funciones.

¿Qué es el plano cartesiano?

Se llama plano cartesiano o sistema cartesiano a un diagrama de coordenadas ortogonales usadas para operaciones geométricas en el espacio euclídeo (o sea, el espacio geométrico que cumple con los requisitos formulados en la antigüedad por Euclides).

Se utiliza para representar gráficamente funciones matemáticas y ecuaciones de geometría analítica. También permite representar relaciones de movimiento y posición física.

Se trata de un sistema bidimensional, constituido por dos ejes que se extienden desde un origen hasta el infinito (formando una cruz). Estos ejes se interceptan en un único punto (que denota el punto de origen de coordenadas o punto 0,0).

Sobre cada eje se trazan un conjunto de marcas de longitud, que sirven de referencia para ubicar puntos, trazar figuras o representar operaciones matemáticas. O sea, es una herramienta geométrica para poner estas últimas en relación gráficamente.

El plano cartesiano debe su nombre al filósofo francés René Descartes (1596-1650), creador del campo de la geometría analítica.

Ver además: Ángulo

Historia del plano cartesiano

El plano cartesiano fue una invención de René Descartes, como hemos dicho, filósofo central en la tradición de Occidente. Su perspectiva filosófica se basó siempre en la búsqueda del punto de origen del conocimiento.

Como parte de esa búsqueda, realizó amplios estudios sobre la geometría analítica, de la cual se considera padre y fundador. Logró trasladar matemáticamente la geometría analítica al plano bidimensional de la geometría plana y dio origen al sistema de coordenadas que aún hoy utilizamos y estudiamos.

¿Para qué sirve el plano cartesiano?

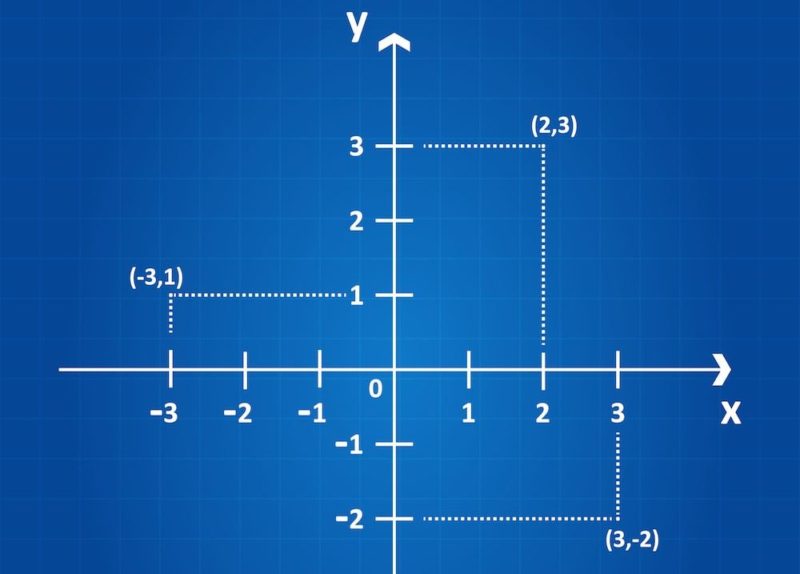
El plano cartesiano es un diagrama en el que podemos ubicar puntos, basándonos en sus coordenadas respectivas en cada eje, tal y como hace un GPS en el globo terráqueo. De allí, también es posible representar gráficamente el movimiento (el desplazamiento de un punto a otro en el sistema de coordenadas).

Además, permite trazar figuras geométricas bidimensionales a partir de rectas y curvas. Estas figuras se corresponden con determinadas operaciones aritméticas, como ecuaciones, operaciones simples, etc.

Existen dos formas de dar resolución a esas operaciones: de forma matemática y luego graficarla, o bien podemos hallar una solución gráficamente, ya que existe una clara correspondencia entre lo que se ilustra en el plano cartesiano, y aquello que se expresa en símbolos matemáticos.

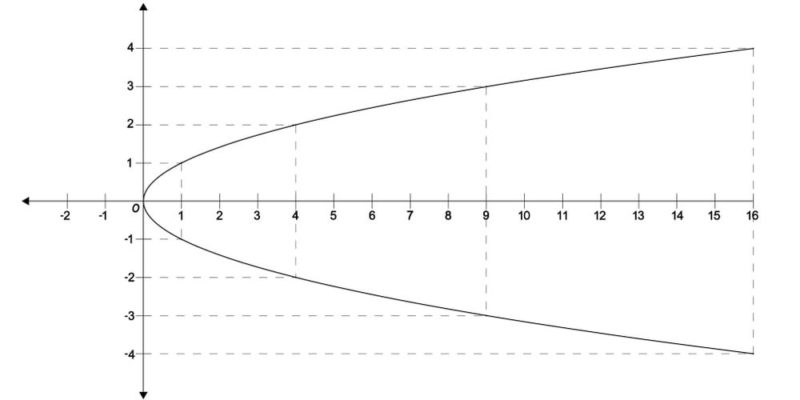
En el sistema de coordenadas, para ubicar los puntos necesitamos dos valores: el primero correspondiente al eje horizontal X y el segundo al eje vertical Y, los cuales se denotan entre paréntesis y separados por una coma: (0,0) por ejemplo, es el punto en donde ambas líneas se cruzan.

Dichos valores pueden ser positivos o negativos, dependiendo de su ubicación respecto a las líneas que conforman el plano.

Cuadrantes del plano cartesiano

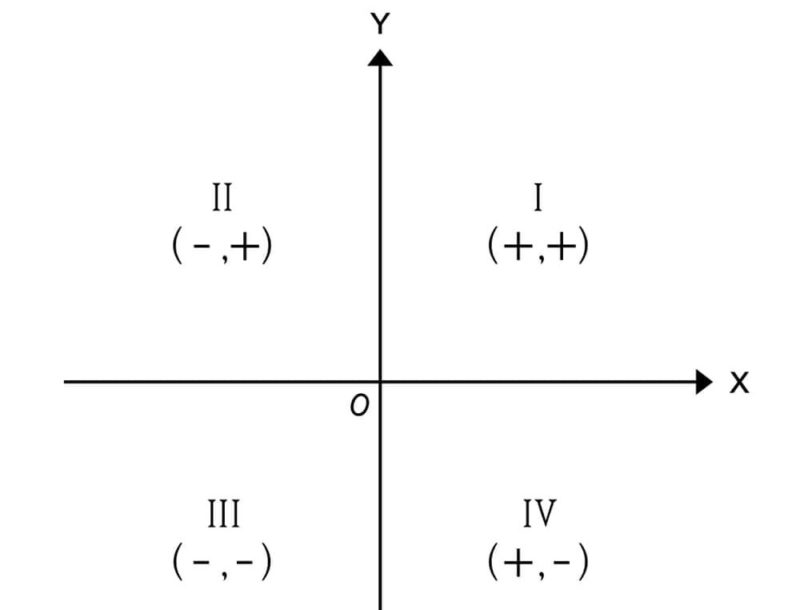
Como hemos visto, el plano cartesiano se constituye por el cruce de dos ejes de coordenadas, o sea, dos líneas rectas infinitas, identificadas con las letras x (horizontal) y por otro lado y (vertical). Si las contemplamos, veremos que conforman una suerte de cruz, dividiendo así el plano en cuatro cuadrantes, que son:

  • Cuadrante I. En la región superior derecha, en donde pueden representarse valores positivos en cada eje de coordenadas. Por ejemplo: (1,1).
  • Cuadrante II. En la región superior izquierda, en donde pueden representarse valores positivos en el eje y pero negativos en el x. Por ejemplo: (-1, 1).
  • Cuadrante III. En la región inferior izquierda, en donde pueden representarse valores negativos en ambos ejes. Por ejemplo: (-1,-1).
  • Cuadrante IV. En la región inferior derecha, en donde pueden representarse valores negativos en el eje y pero positivos en el x. Por ejemplo: (1, -1).

Elementos del plano cartesiano

El plano cartesiano se compone de dos ejes perpendiculares, como ya sabemos: las ordenadas (eje y) y las abscisas (eje x). Ambas rectas se extienden hasta el infinito, tanto en sus valores positivos, como negativos. El único punto de cruce entre ambas se denomina origen (coordenadas 0,0).

A partir del origen cada eje se marca con valores expresados en números enteros. Al punto de intersección de dos puntos cualesquiera, se le llama punto. Cada punto se expresa en sus respectivas coordenadas, siempre diciendo primero las abscisas y luego las ordenadas. Juntando dos puntos se puede construir una recta, y con varias rectas una figura.

Funciones en un plano cartesiano

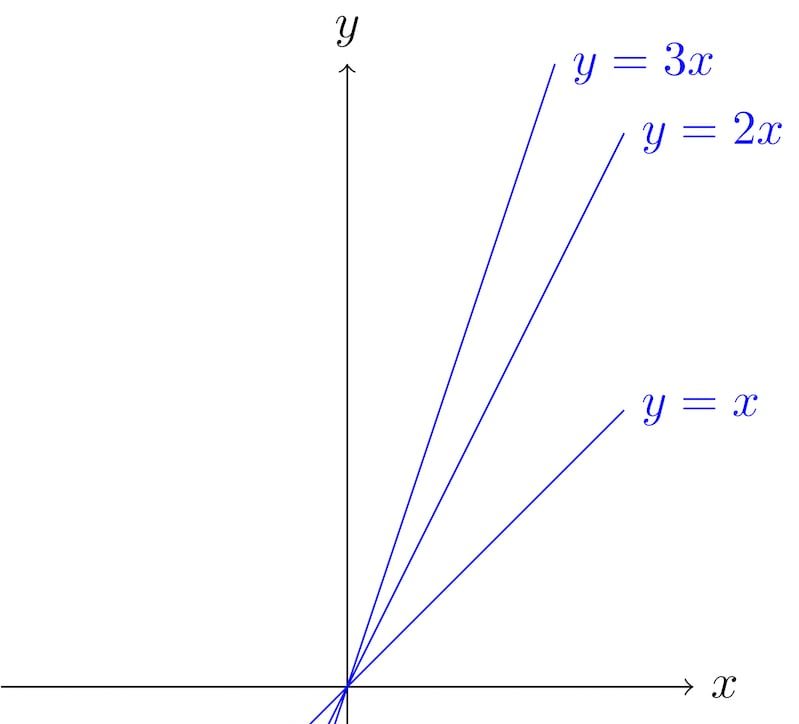
Las funciones matemáticas pueden expresarse gráficamente en un plano cartesiano, siempre y cuando expresemos la relación entre una variable x y una variable y de manera tal que pueda resolverse.

Por ejemplo, si tenemos una función que establece que el valor de y será 4 cuando el de x sea 2, podemos decir que tenemos una función expresable así: y = 2x. La función señala la relación entre ambos ejes, y permite dar valor a una variable conociendo el valor de la otra.

Por ejemplo si x = 1, entonces y = 2. Por otro lado, si x = 2, entonces y = 4, si x = 3, entonces y = 6, etc. al hallar todos esos puntos en el sistema de coordenadas, tendremos una línea recta, dado que la relación entre ambos ejes es continua y estable, predecible. Si continuamos la línea recta hacia el infinito, sabremos entonces cuál será el valor de x en cualquier caso de y.

La misma lógica aplicará para otro tipo de funciones, más complejas, que arrojarán líneas curvas, parábolas, figuras geométricas o líneas discontinuas, dependiendo de la relación matemática expresada en la función. Sin embargo, la lógica seguirá siendo la misma: expresar la función gráficamente en base a asignar valores a las variables y resolver la ecuación.

Referencias