Esfuerzo de tensión: fórmula y ecuaciones, cálculo, ejercicios
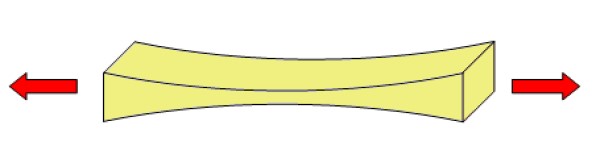
El esfuerzo de tensión se define como la fuerza perpendicular al área por unidad de área aplicada a un objeto en sus extremos para ejercer tracción sobre él, gracias a lo cual se alarga. Sus dimensiones son de fuerza / área y en forma matemática podemos expresarlo así:
τ = F / A
La unidad del esfuerzo en el Sistema Internacional de Unidades es la misma que se utiliza para la presión: el pascal, abreviado Pa, que equivale a 1 newton/ m2.

En el esfuerzo de tensión, se tienen dos fuerzas que se aplican en la misma dirección y sentidos contrarios, las cuales estiran el cuerpo. Si originalmente la longitud del objeto era Lo, al aplicar el esfuerzo de tensión la nueva longitud es L y el estiramiento ΔL se calcula mediante:
ΔL = L – Lo
Los objetos sólidos poseen elasticidad en mayor o menor medida, lo que significa que al desaparecer el esfuerzo de tensión, regresan a sus dimensiones originales.
Esto sucede siempre que el esfuerzo no sea tan grande como para causar deformación permanente. Materiales de goma, caucho o hule son buenos para hacer objetos elásticos y también tienen esta cualidad el cabello y la piel, entre otros.
Índice del artículo
- 1 Deformación unitaria
- 2 ¿Cómo se calcula el esfuerzo de tensión? (Ejemplos)
- 3 Ejercicios resueltos
- 4 – Ejercicio 1
- 5 – Ejercicio 2
- 6 Referencias
Al estudiar cómo se deforman los cuerpos bajo tensión, es muy conveniente definir el concepto de deformación unitaria, una cantidad sin dimensiones. La deformación unitaria se denota mediante la letra griega δ (“delta” minúscula) y se calcula así:
δ = ΔL /Lo
La deformación unitaria sirve para evaluar comparativamente la deformación del objeto bajo tensión. Veámoslo de esta manera: no es igual estirar 1 cm una barra de 1 metro de largo, que estirar 1 cm a otra de 10 m de largo. En el primer caso la deformación es bastante más significativa que en el segundo.
El físico inglés y contemporáneo de Newton llamado Robert Hooke (1635-1703), investigó las propiedades elásticas de los cuerpos y estableció la ley que lleva su nombre. Con ella se relaciona el esfuerzo aplicado con la deformación experimentada cuando el esfuerzo es pequeño:
Esfuerzo ∝ Deformación (unitaria)
Es lógico esperar que a mayor esfuerzo de tensión, mayor alargamiento se producirá. Haciendo uso de las definiciones dadas anteriormente:
τ ∝ δ
La constante de proporcionalidad necesaria para establecer la igualdad se denota Y y se conoce como módulo de Young o módulo de elasticidad, característico de los materiales:
τ = Y⋅δ
El módulo de Young tiene las mismas unidades del esfuerzo de tensión, ya que la deformación unitaria es adimensional.
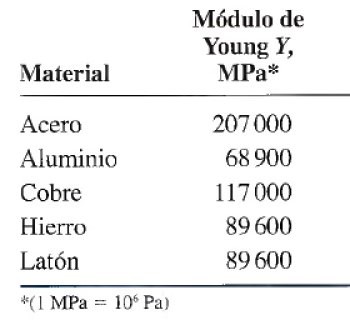
Entonces, una manera de calcular el esfuerzo de tensión en un cuerpo con propiedades elásticas, es midiendo la deformación y conociendo su módulo de Young. Esta cantidad se ha determinado experimentalmente para muchos materiales y está tabulada.
Supongamos que a un alambre hecho de acero templado de 3 mm de diámetro se le somete a un esfuerzo de tensión, colgando de él un peso de 250 N, ¿cuál sería la magnitud de dicho esfuerzo?
Bien, podemos emplear la definición del esfuerzo de tensión como el cociente entre la fuerza perpendicular a la superficie y el área de dicha superficie. Calculemos primero el área, suponiendo un alambre de sección transversal circular:
A = π . (d/2)2 = π . (d2 /4)
El diámetro del alambre es de 3 mm y hay que transformar estas unidades a metros:
d = 3 x 10-3 m.
A = π . (3 x 10-3 m)2 / 4 = 7.07 x 10-6 m2.
El esfuerzo de tensión es producido por el peso que cuelga del alambre, el cual está aplicado en forma perpendicular a la sección transversal del mismo, por lo tanto:
τ = 250 N / 7.07 x 10-6 m2 = 3.5 x 10 7 Pa
El pascal es una unidad bastante pequeña, así que los múltiplos no son inusuales. Sabiendo que 1 mega-pascal (MPa) es 106 pascal, el esfuerzo de tensión queda:
τ = 35 MPa
El módulo de elasticidad de una varilla es de 4 x 1011 Pa. ¿Qué deformación unitaria se obtiene al aplicar un esfuerzo de tensión de 420 MPa?
Solución
La ecuación a utilizar es:
τ = Y⋅δ
Con ella calculamos la deformación unitaria:
δ = τ / Y = 420 x 106 Pa / 4 x 1011 Pa = 0.00105
δ = ΔL /Lo
Por lo tanto la deformación ΔL es:
ΔL = 0.00105 Lo
Si por ejemplo la varilla tenía originalmente 1 metro de largo, con ese esfuerzo de tensión se estira apenas 0.00105 m = 1.05 mm.
Un alambre de acero tiene 1.50 m de longitud y un diámetro de 0.400 mm. Uno de los extremos se sujeta del techo y del otro se coloca un reflector de masa m = 1.50 kg, el cual se suelta. Calcular:
a) El estiramiento del alambre.
b) La deformación unitaria y la deformación unitaria porcentual. ¿Es posible que el alambre se rompa por el peso del reflector?
Solución
El alambre se va a estirar, puesto que al colgar el reflector es sometido a un esfuerzo de tensión. La fuerza que produce dicho esfuerzo es el peso del reflector.
El peso de un objeto de masa m es el producto de la masa por el valor de la aceleración de la gravedad, por lo tanto:
F = 1.50 kg x 9.8 m/s2 = 14.7 N
Se necesita el área de la sección transversal del alambre:
A = π . (d2 /4) = π x (0.4 x 10-3 m)2 / 4 = 1.26 x 10-7 m2.
Con estos resultados se calcula el esfuerzo que ejerce el peso sobre el alambre:
τ = 14.7 N / 1.26 x 10-7 m2 = 1.17 x 108 Pa
El alambre tiene un comportamiento elástico, por lo tanto es válido suponer que se cumple la ley de Hooke:
τ = Y⋅δ
De la tabla de módulos de elasticidad encontramos que para el acero Y= 207 x 109 Pa. Además la deformación unitaria es:
δ = ΔL /Lo
Sustituyendo en la ecuación para el esfuerzo:
τ = Y⋅δ = Y⋅ (ΔL /Lo)
Por lo tanto el estiramiento es:
ΔL = Lo τ / Y =
=1.50 m x 1.17 x 108 Pa / 207 x 109 Pa = 8.5 x 10-4 m = 0.849 mm.
La deformación unitaria del alambre es:
δ = ΔL /Lo = 8.5 x 10-4 m / 1.5 m = 5.652 x 10-4
Si la expresamos en porcentaje, la deformación unitaria porcentual es de 0.0565 %, menor a 0.1 %, por lo tanto es de esperar que el alambre resista bien el peso del reflector sin romperse, ya que la deformación que experimenta no es demasiado grande en comparación a la longitud original.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Beer, F. 2010. Mecánica de materiales. McGraw Hill. 5ta. Edición.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
- Valera Negrete, J. 2005. Apuntes de Física General. UNAM.
