Volumen molar: concepto y fórmula, cálculo y ejemplos

El volumen molar es una propiedad intensiva que indica cuánto espacio ocupa un mol de una determina sustancia o compuesto. Viene representada por el símbolo V_m, y es expresada en unidades de dm³/mol para gases, y cm³/mol para líquidos y sólidos, debido a que estos últimos se hallan más confinados por sus mayores fuerzas intermoleculares.

Esta propiedad es recurrente al momento de estudiar sistemas termodinámicos que involucran a los gases; ya que, para los líquidos y sólidos las ecuaciones para determinar V_m se tornan más complicadas e inexactas. Por lo tanto, en lo que concierne a cursos básicos, el volumen molar siempre está asociado a la teoría de los gases ideales.

Esto se debe a que para los gases ideales o perfectos son irrelevantes los aspectos estructurales; todas sus partículas se visualizan como esferas que colisionan elásticamente entre sí y se comportan del mismo modo sin importar cuáles sean sus masas o propiedades.

Siendo así, un mol de cualquier gas ideal ocupará, a una presión y temperatura determinadas, un mismo volumen V_m. Se dice entonces que en condiciones normales de P y T, 1 atm y 0 ºC, respectivamente, un mol de un gas ideal ocupará un volumen de 22,4 litros. Este valor es útil y aproximado aun cuando se evalúan los gases reales.

Índice del artículo

• 1 Concepto y fórmula
  • 1.1 Para gases
  • 1.2 Para líquidos y sólidos
• 2 ¿Cómo calcular el volumen molar?
• 3 Ejemplos de cálculo del volumen molar
  • 3.1 Ejemplo 1
  • 3.2 Ejercicio 2
  • 3.3 Ejercicio 3
• 4 Referencias

Concepto y fórmula

Para gases

La fórmula inmediata para calcular el volumen molar de una especie es:

V_m = V/n

Donde V es el volumen que ocupa, y n la cantidad de la especie en moles. El problema es que V_m depende de la presión y la temperatura que experimentan las moléculas, y se desea una expresión matemática que tome estas variables en cuenta.

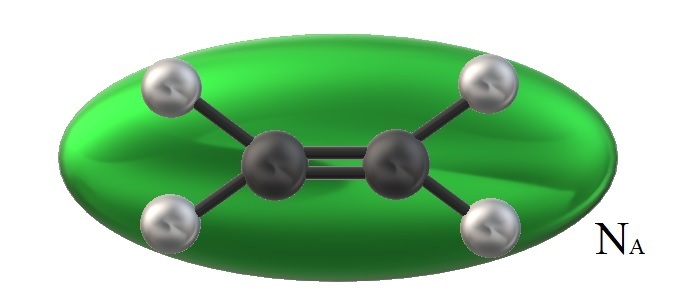
El etileno de la imagen, H₂C=CH₂, tiene un volumen molecular asociado y limitado por un elipsoide verde. Este H₂C=CH₂ puede girar de múltiples formas, que es como si se moviera en el espacio dicho elipsoide para visualizar qué tanto volumen ocuparía (evidentemente despreciable).

No obstante, si el volumen de tal elipsoide verde lo multiplicamos por N_A, el número de Avogadro, tendremos entonces un mol de moléculas de etileno; un mol de elipsoides interaccionando entre sí. A mayor temperatura, las moléculas se separarán unas de otra; mientras que a mayor presión, se contraerán y reducirán su volumen.

Por lo tanto, V_m es dependiente de P y T. El etileno es de geometría plana, por lo que no puede pensarse que su V_m sea precisa y exactamente el mismo que el de metano, CH₄, de geometría tetraédrica y capaz de representarse con una esfera y no un elipsoide.

Para líquidos y sólidos

Las moléculas o átomos de los líquidos y sólidos también tienen su propio V_m, el cual puede relacionarse aproximadamente con su densidad:

V_m = m/(d·n)

La temperatura afecta más el volumen molar para los líquidos y sólidos que la presión, siempre y cuando esta última no varíe bruscamente ni sea exorbitante (en el orden de los GPa). Asimismo, al igual que como se mencionó con el etileno, las geometrías y estructuras moleculares tienen una gran influencia en los valores de V_m.

No obstante, en condiciones normales se observa que las densidades para distintos líquidos o sólidos no varían demasiado en sus magnitudes; lo mismo ocurre con sus volúmenes molares. Nótese que mientras más denso sean, menor será V_m.

Respecto a los sólidos, su volumen molar también depende de sus estructuras cristalinas (el volumen de su celda unitaria).

¿Cómo calcular el volumen molar?

A diferencia de los líquidos y sólidos, para los gases ideales sí hay una ecuación que permite calcular V_m en función de P y T y sus cambios; esta es, la de los gases ideales:

P = nRT/V

La cual se va acomodando para expresar V/n:

V/n = RT/P

V_m =  RT/P

Si utilizamos la constante de los gases R= 0,082 L·atm·K^-1·mol^-1, entonces las temperaturas deberán venir expresadas en kelvin (K), y las presiones en atmósferas. Nótese que aquí se observa por qué V_m es una propiedad intensiva: T y P no tienen nada que ver con la masa del gas pero sí con su volumen.

Estos cálculos solo son  válidos en condiciones donde los gases se comportan cercanamente a la idealidad. Sin embargo, los valores obtenidos mediante la experimentación tienen un margen de error pequeño en relación a los teóricos.

Ejemplos de cálculo del volumen molar

Ejemplo 1

Se tiene un gas Y cuya densidad es 8,5·10^-4 g/cm³. Si se tienen 16 gramos equivalentes a 0,92 moles de Y, calcule su volumen molar.

A partir de la fórmula de la densidad podemos calcular qué volumen de Y ocupan tales 16 gramos:

V = 16 g/ (8,5·10^-4 g/cm³)

= 18.823,52 cm³ o 18,82 L

Por lo que V_m se calcula directamente dividiendo este volumen entre la cantidad de moles dados:

V_m = 18,82 L/0,92 mol

= 20,45 L/mol o L·mol^-1 o dm³·mol^-1

Ejercicio 2

En el ejemplo anterior de Y no se especificó en ningún momento cuál era la temperatura que experimentaban las partículas de dicho gas. Asumiendo que se trabajó con Y a presión atmosférica, calcule la temperatura necesaria para comprimirlo al volumen molar determinado.

El enunciado del ejercicio es más largo que su resolución. Recurrimos a la ecuación:

V_m =  RT/P

Pero despejamos T, y sabiendo que la presión atmosférica es 1 atm, resolvemos:

T = V_mP/R

= (20,45 L/mol)(1 atm)/(0,082 L·atm/K·mol)

= 249,39 K

Es decir, un mol de Y ocupará 20,45 litros a una temperatura cercana a -23,76 ºC.

Ejercicio 3

Siguiendo los resultados anteriores, determine V_m a 0 ºC, 25 ºC y en el cero absoluto a la presión atmosférica.

Transformando las temperaturas a kelvin, tenemos primero 273,17 K, 298,15 K y 0 K. Resolvemos directamente sustituyendo para la primera y segunda temperaturas:

V_m = RT/P

= (0,082 L·atm/K·mol)(273,15 K)/ 1 atm

=22,40 L/mol (0 ºC)

= (0,082 L·atm/K·mol)(298,15 K)/ 1 atm

= 24,45 L/mol (25ºC)

El valor de 22,4 litros se mencionó al principio. Nótese cómo V_m incrementa con la temperatura. Cuando se quiere hacer el mismo cálculo con el cero absoluto, nos tropezamos con la tercera ley de la termodinámica:

(0,082 L·atm/K·mol)(0 K)/ 1 atm

= 0 L/mol (-273,15 ºC)

El gas Y no puede tener un volumen molar inexistente; eso quiere decir que se ha transformado en un líquido y ya no tiene validez la ecuación anterior.

Por otro lado, la imposibilidad de calcular V_m en el cero absoluto obedece la tercera ley de la termodinámica, la cual dice que es imposible enfriar cualquier sustancia a la temperatura del cero absoluto.

Referencias

1. Ira N. Levine. (2014). Principios de Fisicoquímica. Sexta edición. Mc Graw Hill.
2. Glasstone. (1970). Tratado de química física. Segunda edición. Aguilar.
3. Wikipedia. (2019). Molar volume. Recuperado de: en.wikipedia.org
4. Helmenstine, Anne Marie, Ph.D. (08 de agosto de 2019). Molar Volume Definition in Chemistry. Recuperado de: thoughtco.com
5. BYJU’S. (2019). Molar Volume Formula. Recuperado de: byjus.com
6. González Mónica. (28 de octubre de 2010). Volumen molar. Recuperado de: quimica.laguia2000.com