Esfuerzo normal: en qué consiste, cómo se calcula, ejemplos
El esfuerzo normal aplicado sobre un cierto material, también denominado esfuerzo uniaxial, es la relación que existe entre la fuerza aplicada perpendicularmente sobre cierta superficie y el área de sección transversal sobre la que actúa, o bien la carga por unidad de área. Matemáticamente, si P es la magnitud de la fuerza y A es el área donde está aplicada, el esfuerzo σ es el cociente: σ = P/A.
Las unidades del esfuerzo normal en el Sistema Internacional son newton /metro2, conocidas como Pascales y abreviadas Pa. Se trata de las mismas unidades de la presión. Otras unidades que aparecen en la literatura frecuentemente son las libras / pulgada2 o psi.

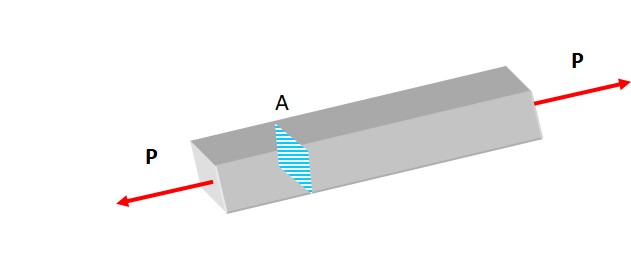
En la figura 2 dos fuerzas de igual magnitud están aplicadas perpendicularmente al área de sección transversal, efectuando una tracción sobre la barra muy liviana que tiende a alargarla.
Dichas fuerzas producen un esfuerzo normal que también se denomina carga axial centrada, a causa de que su línea de acción coincide con el eje axial, sobre el cual se encuentra el centroide.
Los esfuerzos, ya sean normales o de otros tipos, aparecen continuamente en la naturaleza. En la litosfera, las rocas están sometidas a la gravedad y a la actividad tectónica, experimentando deformaciones.
De esta manera se originan estructuras tales como pliegues y fallas, cuyo estudio es importante en el aprovechamiento de minerales y en ingeniería civil, para la construcción de edificaciones y carreteras, por citar unos pocos ejemplos.
Índice del artículo
- 1 ¿Cómo se calcula?
- 2 La ley de Hooke y el esfuerzo normal
- 3 Importancia del esfuerzo en la resistencia de los materiales y la geología
- 4 Ejemplos
- 5 Referencias
La ecuación dada al comienzo σ = P/A permite calcular el esfuerzo normal promedio sobre el área en cuestión. El valor de P es la magnitud de la fuerza resultante sobre el área aplicada al centroide y es suficiente para muchas situaciones sencillas.
En tal caso, la distribución de fuerzas es uniforme, sobre todo en puntos alejados de donde se tiene la barra sujeta a la tracción o compresión. Pero si se necesita calcular el esfuerzo en un punto concreto o las fuerzas no se distribuyen uniformemente es preciso emplear la definición siguiente:
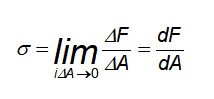
Entonces en general, el valor del esfuerzo en un punto en particular puede ser diferente del valor promedio. De hecho el esfuerzo puede variar según la sección a considerar.
Esto se ilustra en la siguiente figura, en la cual las fuerzas de tracción F intentan separar a la barra en equilibrio en las secciones mm y nn.
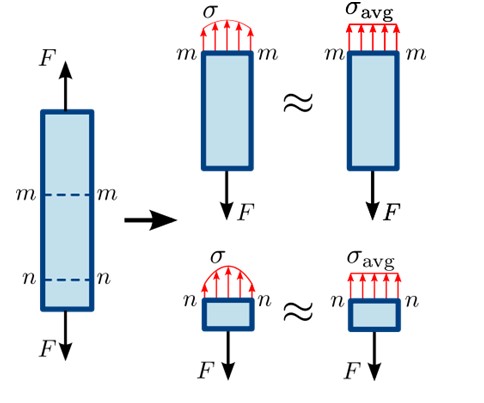
Como la sección nn está muy cerca de donde se aplica la fuerza F hacia abajo, la distribución de fuerzas sobre la superficie no es del todo homogénea, siendo estas menores cuanto más lejos se esté de dicho punto. La distribución es un poco más homogénea en la sección mm.
En todo caso el esfuerzo normal siempre tiende a estirar o a comprimir las dos partes del cuerpo que se encuentran a ambos lados del plano sobre el cual actúan. En cambio otros esfuerzos diferentes, como el de cizalla, tienden a desplazar y separar estas partes.
La ley de Hooke afirma que dentro de los límites elásticos, el esfuerzo normal es directamente proporcional a la deformación experimentada por la barra o el objeto. En tal caso:
Esfuerzo normal ∝ Deformación unitaria
Siendo la constante de proporcionalidad el módulo de Young (Y):
Esfuerzo normal (σ) = Módulo de Young (Y) x Deformación unitaria (ε)
σ = Y. ε
Con ε = ΔL/L, donde ΔL es la diferencia entre la longitud final y la inicial, que es L.
El módulo de Young o módulo de elasticidad es una característica propia del material, cuyas dimensiones son las mismas que las del esfuerzo, puesto que la deformación unitaria es adimensional.
Determinar cómo de resistentes son los materiales ante los esfuerzos es muy importante. Para las estructuras utilizadas en la construcción de edificaciones, así como en el diseño de piezas para distintos dispositivos, hay que asegurarse de que los materiales elegidos cumplan adecuadamente su función.
Por ello los materiales se analizan exhaustivamente en los laboratorios mediante ensayos destinados a saber cuánta fuerza pueden resistir antes de deformarse y de romperse, perdiendo así sus funciones. Con base a ello se toma la decisión de si son aptos o no para fabricar cierta pieza o formar parte de un dispositivo.
Se cree que el primer científico en estudiar sistemáticamente la resistencia de los materiales fue Leonardo Da Vinci. Él dejó evidencia de ensayos en los que determinaba la resistencia de alambres colgándoles piedras de distintos pesos.
En los esfuerzos tanto la magnitud de la fuerza como también las dimensiones de la estructura y de qué forma es aplicada es importante, para así establecer los límites dentro de los cuales el material tiene un comportamiento elástico; es decir, regresa a su forma original cuando el esfuerzo cesa.
Con los resultados de estas pruebas se realizan curvas de esfuerzo-deformación para distintos tipos de materiales, como acero, hormigón, aluminio y muchos más.
En los ejemplos siguientes se supone que las fuerzas está distribuidas uniformemente, y que el material es homogéneo e isótropo. Esto significa que sus propiedades son las mismas en cualquier dirección. Por lo tanto es válido aplicar la ecuación σ = P/A para encontrar los esfuerzos.
En la figura 3, se sabe que el esfuerzo normal promedio actuando sobre el tramo AB tiene magnitud 48 kPa. Encontrar: a) La magnitud de la fuerza F que actúa en CB, b) El esfuerzo sobre el tramo BC.
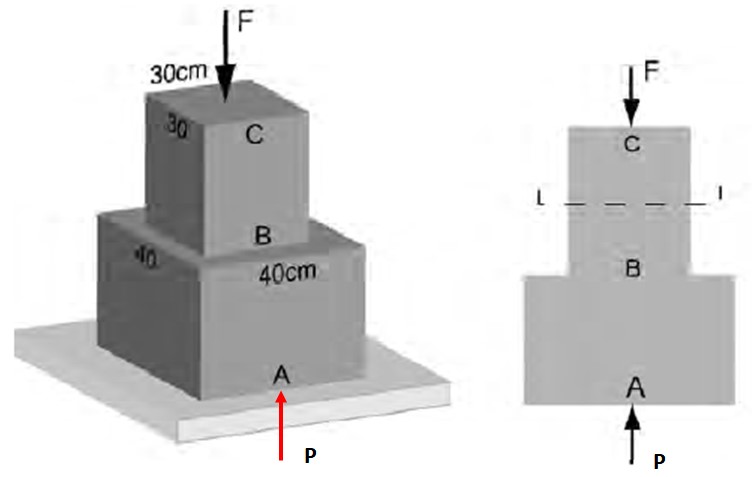
Solución
Puesto que la estructura está en equilibrio estático, de acuerdo a la segunda ley de Newton:
P-F = 0
El esfuerzo normal sobre la sección AB tiene magnitud:
σAB = P/AAB
De donde P = σAB . AAB = 48000 Pa. (40 x 10 -2 m)2 = 7680 N
Por lo tanto F = 7680 N
El esfuerzo normal sobre el tramo BC es el cociente entre la magnitud de F y el área de la sección transversal de ese lado:
σBC = F/ABC = 7680 N / (30 x 10 -2 m)2 = 85.3 kPa.
Un alambre de 150 m de longitud y 2.5 mm de diámetro es estirado mediante una fuerza de 500 N. Encontrar:
a) El esfuerzo longitudinal σ.
b) La deformación unitaria, sabiendo que la longitud final es 150.125 m.
c) El módulo de elasticidad Y de este alambre.
Solución
a) σ = F/A = F / π.r2
El radio del alambre es la mitad del diámetro:
r = 1.25 mm = 1.25 x 10-3 m.
El área de la sección transversal es π.r2, luego el esfuerzo es:
σ= F / π.r2 = 500 / (π.(1.25 x 10-3)2 Pa= 101859.2 Pa
b) ε = ΔL/L = (Longitud final – Longitud inicial) / Longitud inicial
Por lo tanto:
ε = (150.125 – 150) /150 = 0.125 / 150 = 0.000833
c) El módulo de Young del alambre se despeja conociendo los valores de ε y σ previamente calculados:
Y = σ / ε = 101859.2 Pa / 0.000833 = 1.22 x 108 Pa = 122 MPa.
- Beer, F. 2010. Mecánica de materiales. 5ta. Edición. McGraw Hill. 7 – 9.
- Giancoli, D. 2006. Physics: Principles with Applications. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mecánica de materiales. 6ta. Edición. Pearson Educación. 22 -25
- Valera Negrete, J. 2005. Apuntes de Física General. UNAM. 87-98.
- Wikipedia. Stress (Mechanics). Recobrado de: wikipedia.org.
