Elipsoide: características y ejemplos
El elipsoide es una superficie en el espacio que pertenece al grupo de las superficies cuádricas y cuya ecuación general es de la forma:
Ax2 + By2 + Cz2 + Dxy +Exz + Fyz+Gx + Hy + Iz + J =0
Es el equivalente tridimensional de una elipse, caracterizada por tener trazas elípticas y circulares en algunos casos especiales. Las trazas son las curvas que se obtienen al intersectar el elipsoide con un plano.
Además del elipsoide, hay otras cinco cuádricas más: hiperboloide de una hoja y dos hojas, dos tipos de paraboloide (hiperbólico y elíptico) y el cono elíptico. Sus trazas también son cónicas.
El elipsoide también puede expresarse mediante la ecuación estándar en coordenadas cartesianas. Un elipsoide centrado en el origen (0,0,0) y expresado en esta forma, recuerda a la elipse, pero con un término adicional:
Los valores de a, b y c son números reales mayores que 0 y representan los tres semiejes del elipsoide.
Índice del artículo
La ecuación estándar en coordenadas cartesianas para la elipse centrada en el punto (h,k,m) es:
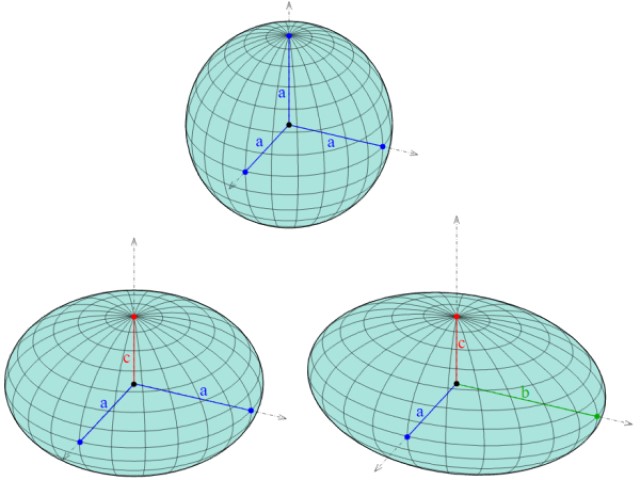
En coordenadas esféricas, el elipsoide puede ser descrito de la siguiente forma:
x = a sen θ. cos φ
y = b sen θ. sen φ
z = c cos θ
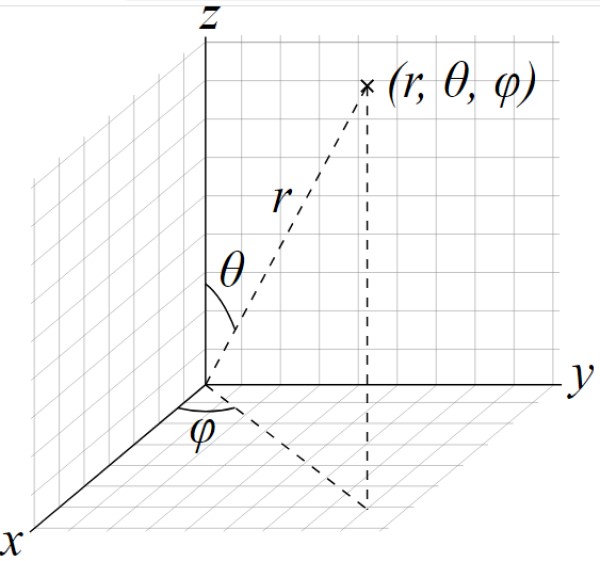
Los semiejes del elipsoide siguen siendo a, b y c, en tanto que los parámetros son los ángulos θ y φ de la siguiente figura:
La ecuación general de una superficie en el espacio es F(x,y, z) = 0 y las trazas de la superficie son las curvas:
– x = c; F(c, y, z) = 0
– y = c; F(x, c, z) = 0
– z = c; F(x, y, c) = 0
En el caso de un elipsoide, tales curvas son elipses y algunas veces circunferencias.
El volumen V del elipsoide está dado por (4/3)π veces el producto de sus tres semiejes:
V= (4/3)π. abc
-Un elipsoide se convierte en una esfera cuando todos los semiejes son del mismo tamaño: a = b = c ≠ 0. Esto tiene sentido, pues el elipsoide es como una esfera a la cual se ha estirado de forma diferente a lo largo de cada eje.
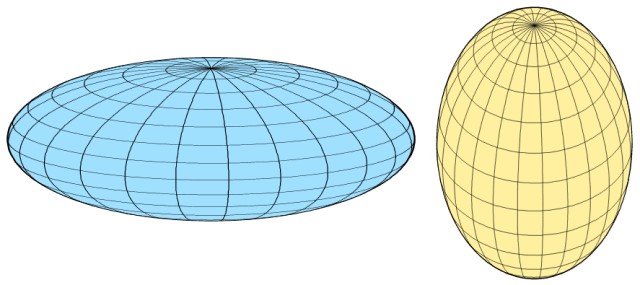
-El esferoide es un elipsoide en el cual dos de los semiejes son idénticos y el tercero es diferente, por ejemplo podría ser a = b ≠ c.
Al esferoide también se le llama elipsoide de revolución, porque se puede generar haciendo rotar elipses alrededor de un eje.
Si el eje de giro coincide con el eje mayor, el esferoide es prolato, pero si coincide con el eje menor, es oblato:
La medida del aplanamiento del esferoide (elipticidad) viene dada por la diferencia de longitud entre los dos semiejes, expresada en forma fraccionaria, es decir, se trata del aplanamiento unitario, dado por:
f = (a – b) / a
En esta ecuación, a representa el semieje mayor y b el semieje menor, recordemos que el tercer eje es igual a alguno de estos para un esferoide. El valor de f está comprendido entre 0 y 1 y para un esferoide tiene que ser mayor que 0 (si fuera igual a 0 tendríamos simplemente una esfera).
Los planetas y en general los astros, no suelen ser esferas perfectas, porque el movimiento de rotación alrededor de sus ejes achata al cuerpo en los polos y lo abulta en el ecuador.
Por eso la Tierra resulta ser como un esferoide oblato, aunque no tan exagerado como el de la anterior figura, y por su parte el gigante gaseoso Saturno es el más achatado de los planetas en el sistema solar.
Así que una forma más realista de representar los planetas, es suponer que son como un esferoide o elipsoide de revolución, cuyo semieje mayor es el radio ecuatorial y el semieje menor el radio polar.
Cuidadosas medidas hechas sobre el globo terráqueo han permitido construir el elipsoide de referencia de la Tierra como su forma más precisa para trabajarla matemáticamente.
Las estrellas también tienen movimientos de rotación que les confieren formas más o menos achatadas. La veloz estrella Achernar, la octava estrella más brillante del cielo nocturno, en la constelación austral de Eridanus es notablemente elíptica al compararla con la mayoría. Está a 144 años luz de nosotros.
En el otro extremo, hace pocos años los científicos dieron con el objeto más esférico encontrado hasta ahora: la estrella Kepler 11145123, a 5000 años luz, con un tamaño dos veces el de nuestro Sol y una diferencia entre los semiejes de apenas 3 km. Como era de esperar, también gira más despacio.
En cuanto a la Tierra, tampoco es un esferoide perfecto a causa de su accidentada superficie y las variaciones locales de la gravedad. Por eso existe más de un esferoide de referencia disponible y en cada sitio se elige el más adecuado a la geografía local.
La ayuda de los satélites es inestimable en cuanto a crear modelos cada vez más precisos de la forma de la Tierra, gracias a ellos se sabe por ejemplo que el polo sur es más cercano al ecuador que el polo norte.

Debido a la rotación de la Tierra se genera una fuerza centrífuga que le otorga la forma de un elipsoide oblongo, en lugar de una esfera. Se sabe que el radio ecuatorial de la Tierra es de 3963 millas y el radio polar es 3942 millas.
Encontrar la ecuación de la traza ecuatorial, la de este elipsoide y la medida de su aplanamiento. Además comparar con la elipticidad de Saturno, con los datos que se suministran a continuación:
-Radio ecuatorial de Saturno: 60268 km
-Radio polar de Saturno: 54364 km
Solución
Se requiere un sistema de coordenadas, el cual supondremos centrado en el origen (centro de la Tierra). Supondremos el eje z vertical y la traza que corresponde al ecuador se encuentra sobre el plano xy, equivalente al plano z = 0.
En el plano ecuatorial los semiejes a y b son iguales, por lo tanto a = b = 3963 millas, mientras que c = 3942 millas. Se trata de un caso especial: un esferoide centrado en el punto (0,0,0) como se dijo anteriormente.
La traza ecuatorial es una circunferencia de radio R= 3963 millas, centrada en el origen. Se calcula haciendo z = 0 en la ecuación estándar:
Y la ecuación estándar del elipsoide terrestre es:
f Tierra = (a – b) / a = (3963-3942) millas /3963 millas = 0.0053
f Saturno = (60268-54363)km/60268 km = 0.0980
Nótese que la elipticidad f es una cantidad adimensional.
- ArcGIS for Desktop. Esferoides y esferas. Recuperado de: desktop.arcgis.com.
- BBC Mundo. El misterio del objeto más esférico jamás descubierto en el Universo. Recuperado de: bbc.com.
- Larson, R. Cálculo y Geometría Analítica. Sexta edición. Volumen 2. McGraw Hill.
- Wikipedia. Ellipsoid. Recuperado de: en.wikipedia.org.
- Wikipedia. Spheroid. Recuperado de: en.wikipedia.org.
