Números imaginarios: propiedades, aplicaciones, ejemplos

Los números imaginarios son aquellos que dan solución a la ecuación en la cual la incógnita, elevada al cuadrado, es igual a un número real negativo. La unidad imaginaria es i = √(-1).

En la ecuación: z²= – a, z es  un número imaginario que se expresa de la siguiente manera:

 z = √(-a) = i√(a)

Siendo a un número real positivo. Si a=1, entonces z = i, donde i es la unidad imaginaria.

En general un número imaginario puro z se expresa siempre de la forma: 

z = y⋅i

Donde y es un número real e i es la unidad imaginaria.

Así como los números reales se representan en una recta, llamada la recta real, de forma análoga los números imaginarios se representan sobre la recta imaginaria.

La recta imaginaria siempre es ortogonal (forma 90º) a la recta real y las dos rectas definen un plano cartesiano llamado el plano complejo.

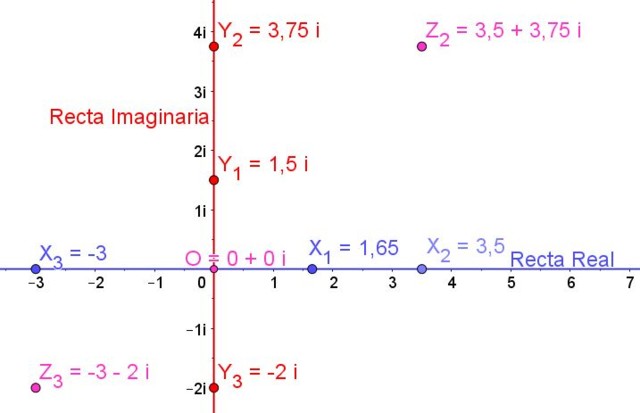
En la figura 1 se muestra el plano complejo y sobre él se representan algunos números reales, algunos números imaginarios y también algunos números complejos:

X₁, X₂, X₃ son números reales

Y₁, Y₂, Y₃ son números imaginarios

Z₂ y Z₃ son números complejos

El número O es el cero real y también es el cero imaginario, por lo que el origen O es el cero complejo expresado por:

0 + 0i 

Índice del artículo

• 1 Propiedades
  • 1.1 Suma y resta de imaginarios
  • 1.2 Producto de imaginarios
  • 1.3 Producto de un número real por otro imaginario
  • 1.4 Potenciación de un imaginario
  • 1.5 Suma de un número real y uno imaginario
• 2 Aplicaciones
• 3 Ejercicios con números imaginarios
  • 3.1 – Ejercicio 1
  • 3.2 – Ejercicio 2
  • 3.3 – Ejercicio 3
  • 3.4 – Ejercicio 4
  • 3.5 – Ejercicio 5
  • 3.6 – Ejercicio 6
• 4 Referencias

Propiedades

El conjunto de los números imaginarios se denota por:

I = { ……, -3i,…,-2i,….,-i,….,0i,….,i,….,2i,….,3i, ……}

Y se pueden definir algunas operaciones sobre este conjunto numérico. No siempre se obtiene un número imaginario a partir de estas operaciones, así que vamos a verlas con un poco más de detalles:

Suma y resta de imaginarios

Los números imaginarios pueden sumarse y restarse entre sí y como resultado se tendrá un nuevo número imaginario. Por ejemplo:

 3i + 2i = 5i

4i – 7i = -3i

Producto de imaginarios

Cuando se efectúa el producto de un número imaginario con otro, el resultado es un número real. Hagamos la siguiente operación para comprobarlo:

2i x 3i = 6 x i² = 6 x (√(-1))² = 6 x (-1) = -6.

Y como vemos, el -6 es un número real, aunque se haya obtenido multiplicando dos números imaginarios puros.

Producto de un número real por otro imaginario

Si se multiplica un número real por i, el resultado será un número imaginario, que corresponde a una rotación de 90 grados en sentido antihorario.

Y es que i² corresponde a dos rotaciones consecutivas de 90 grados, que es equivalente a multiplicar por -1, es decir i² = -1. Se puede apreciar en el siguiente diagrama:

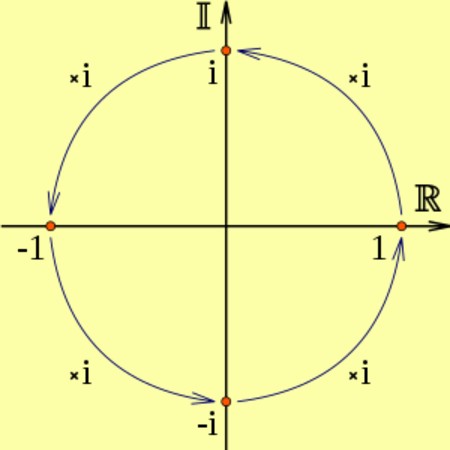
Por ejemplo:

-3 x 5i = -15i

-3 x i = -3i.

Potenciación de un imaginario

Se puede definir la potenciación de un número imaginario a un exponente entero:

i¹ = i

i² = i x i = √(-1) x √(-1) = -1

i³ = i x i² = -i

i⁴ = i² x i² = -1 x -1 = 1

i⁵ = i x i⁴ = i

En general se tiene que iⁿ = i^(n mod 4), donde mod es el residuo de la división entre n y 4.

También puede realizarse la potenciación de enteros negativos:

i^-1 = 1 / i¹ = i / (i x i¹) = i / (i²) = i / (-1) = -i

i-² = 1 / i² = 1/ (-1) = -1

i-³= 1 / i³ = 1 /(-i) = (-1) / i = -1 x i^-1 = (-1)x (-i) = i

En general el número imaginario b⋅i elevado a la potencia n es:

(b⋅i)iⁿ = bⁿ iⁿ = bⁿ i^(n mod 4)

Algunos ejemplos son los siguientes:

(5 i)¹² = 5¹² i¹² = 5¹² i⁰ = 5¹² x 1 = 244140625

(5 i)¹¹ = 5¹¹ i¹¹ = 5¹¹ i³ = 5¹¹ x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ i¹⁰ = 2¹⁰ i² = 1024 x (-1) = -1024

Suma de un número real y uno imaginario

Cuando se suma un número real con uno imaginario, el resultado no es ni real ni imaginario, es un nuevo tipo de número llamado número complejo.

Por ejemplo, si X= 3,5 y Y= 3,75i, entonces el resultado es el número complejo:

Z = X + Y = 3,5 + 3,75 i

Note que en la suma no pueden agruparse las partes real e imaginarias, por eso un número complejo siempre tendrá una parte real y otra parte imaginaria.

Esta operación extiende el conjunto de los números reales al más amplio de los números complejos.

Aplicaciones

El nombre de números imaginarios lo propuso el matemático francés René Descartes (1596-1650) como una burla o desacuerdo con la propuesta de los mismos hecha por el matemático italiano del siglo Raffaelle Bombelli.

Otros grandes matemáticos, como Euler y Leibniz, secundaron a Descartes en este desacuerdo y denominaron a los números imaginarios como números anfibios, que se debatían entre el ser y la nada.

El nombre de números imaginarios se mantiene hoy en día, pero su existencia e importancia es muy real y palpable, ya que aparecen en forma natural en muchos campos de la física como lo son:

-La teoría de la relatividad.

-En el electromagnetismo.

-La mecánica cuántica.

Ejercicios con números imaginarios

– Ejercicio 1

Encontrar las soluciones de la siguiente ecuación:

z² + 16 = 0

Solución

z² = -16

Tomando raíz cuadrada en ambos miembros se tiene:

√(z² ) = √(-16)

± z = √(-1 x 16) = √(-1) √(16) = i x 4 = 4i

Es decir que las soluciones de la ecuación original son:

z = +4i o z = -4i.

– Ejercicio 2

Hallar el resultado de elevar la unidad imaginaria a la potencia 5 menos la resta la unidad imaginaria elevada a la potencia -5.

Solución

i⁵ – i-⁵ = i⁵ – 1/i⁵ = i – 1/i = i – (i)/(i x i) = i – i/(-1) = i + i = 2i

– Ejercicio 3

Hallar el resultado de la siguiente operación:

(3i)³ + 9i 

Solución

3³ i³ – 9 = 9 (-i) + 9i = -9i + 9i = 0i

– Ejercicio 4

Hallar las soluciones de la siguiente ecuación cuadrática:

(-2x)² + 2 = 0

Solución

Se reordena la ecuación de la siguiente manera:

(-2x)² = -2

Seguidamente se toma raíz cuadrada en ambos miembros

√((-2x)²) = √(-2)

± (-2x) = √(-1 x 2) = √(-1) √(2) = i √(2) = √2 i

Luego se despeja x para finalmente obtener:

x = ±√2 / 2 i

Es decir, hay dos soluciones posibles:

x = (√2 / 2) i

O bien esta otra:

x = – (√2 / 2) i

– Ejercicio 5

Hallar el valor de Z definido por:

Z = √(-9) √(-4) + 7

Solución

Sabemos que la raíz cuadrada de un número real negativo es un número imaginario, por ejemplo √(-9) es igual a √(9) x √(-1) = 3i.

Por otra parte, √(-4) es igual a  √(4) x √(-1) = 2i.

De modo que la ecuación original puede sustituirse por:

3i x 2i – 7 = 6 i² – 7 = 6 (-1) – 7 = -6 – 7 = -13

– Ejercicio 6

Encontrar el valor de Z resultante de la siguiente división de dos números complejos:

Z = (9 – i²) / (3 + i)

Solución

El numerador de la expresión puede factorizarse usando la propiedad siguiente:

Una diferencia de cuadrados es el producto de la suma por la diferencia de los binomios sin elevar al cuadrado.

Entonces:

Z = [(3 – i) (3 + i)] / (3 + i)

A continuación se simplifica la expresión resultante quedando

Z = (3 – i)

Referencias

1. Earl, R. Complex numbers. Recuperado de: maths.ox.ac.uk.
2. Figuera, J. 2000. Matemática 1ro. Diversificado. ediciones CO-BO.
3. Hoffmann, J. 2005. Selección de temas de Matemática. Publicaciones Monfort.
4. Jiménez, R. 2008. Álgebra. Prentice Hall.
5. Wikipedia. Imaginary number. Recuperado de: en.wikipedia.org