Transformada discreta de Fourier: propiedades, aplicaciones, ejemplos
La transformada discreta de Fourier es un método numérico utilizado para definir muestreos referentes a las frecuencias espectrales que componen una señal. Estudia funciones periódicas en parámetros cerrados, arrojando como resultado otra señal discreta.
Para poder obtener la transformada discreta de Fourier de N puntos, sobre una señal discreta, se deben cumplir las siguientes 2 condiciones sobre una secuencia x [n]
x [n] = 0 n 0 ˄ n > N – 1
Cumpliéndose estas condiciones se puede definir la transformada discreta de Fourier como
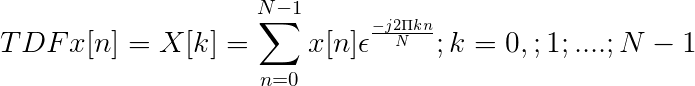
Se puede definir a la transformada discreta de Fourier como un muestreo en N puntos de la transformada de Fourier.
Índice del artículo
- 1 Interpretación de la transformada discreta de Fourier
- 2 Propiedades
- 3 Similitudes y diferencias con la transformada de Fourier
- 4 ¿Para qué sirve la transformada discreta de Fourier?
- 5 Historia
- 6 Transformada discreta de Fourier y su inversa
- 7 Enventanado
- 8 Aplicaciones
- 9 La serie de Fourier
- 10 Otras formas de la serie de Fourier
- 11 Ejemplos
- 12 Ejercicios
- 13 Referencias

Existen 2 puntos de vista desde los cuales se pueden interpretar los resultados obtenidos sobre una secuencia xs[n] a través de la transformada discreta de Fourier.
-El primero corresponde a los coeficientes espectrales, ya conocidos de la serie de Fourier. Se observa en señales periódicas discretas, con muestreos coincidentes con la secuencia xs[n].
-La segunda trata sobre el espectro de una señal aperiódica discreta, con muestreos correspondientes a la secuencia xs[n].
La transformada discreta es una aproximación al espectro de la señal analógica original. Su fase depende de los instantes de muestreo, mientras que su magnitud depende del intervalo de muestreo.
Los fundamentos algebraicos de estructura componen las bases lógicas de los siguientes apartados.
C . Sn → C . F[Sk]; Si una secuencia está multiplicada por un escalar, su transformada también lo estará.
Tn + Vn = F[Tk]+F[Vk] ; La transformada de una suma es igual a la suma de las transformadas.
F[Sn] → (1/N) S-k; Si a una expresión ya transformada se le recalcula la transformada discreta de Fourier, se obtiene la misma expresión, escalada en N e invertida respecto al eje vertical.
Persiguiendo objetivos similares que en la transformada de Laplace, la convolución de funciones se refiere al producto entre sus transformadas de Fourier. La convolución también aplica para tiempos discretos y es responsable de muchos procedimientos modernos.
Xn * Rn → F[Xn] .F[Rn] ; La transformada de una convolución es igual al producto de las transformadas.
Xn . Rn→ F[Xn] * F[Rn] ; La transformada de un producto es igual a la convolución de las transformadas.
Xn-m → F[Xk] e –i(2π/N)km ; Si una sucesión se retrasada en m muestras, su efecto en la transformada discreta será una modificación del ángulo definida por (2π/N)km.
Xt [-k] = X*t[k] = Xt [ N – K ]
W-nmN . x[n] ↔ Xt[k – m]
x[n]y[n] ↔ (1/N) Xt[k]*Yt[k]
X[-n] ↔ Xt[-k] = X*t[k]
x*[n] ↔ X*t[-k]
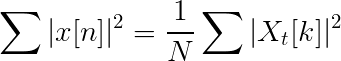
Con respecto a la transformada convencional de Fourier posee varias similitudes y diferencias. La transformada de Fourier convierte una secuencia en una línea continua. De esta forma se dice que el resultado de la variable de Fourier es una función compleja de variable real.
La transformada discreta de Fourier a diferencia, recibe una señal discreta y la transforma en otra señal discreta, es decir una secuencia.
Sirven principalmente para simplificar de manera notable las ecuaciones, mientras transforma expresiones derivadas en elementos de potencia. Denotando expresiones diferenciales en formas de polinomios integrables.
En la optimización, modulación y modelación de resultados actúa como expresión estandarizada, siendo un recurso frecuente para la ingeniería tras varias generaciones.

Este concepto matemático fue presentado por Joseph B. Fourier en el año 1811, mientras desarrollaba un tratado referente a la propagación de calor. Rápidamente fue adoptado por diversas ramas de la ciencia e ingeniería.
Se estableció como principal herramienta de trabajo en el estudio de las ecuaciones con derivadas parciales, comparándose incluso con la relación de trabajo existente entre la transformada de Laplace y las ecuaciones diferenciales ordinarias.
Toda función que pueda ser trabajada con transformada de Fourier debe presentar nulidad fuera de un parámetro definido.
La transformada discreta se obtiene a través de la expresión:
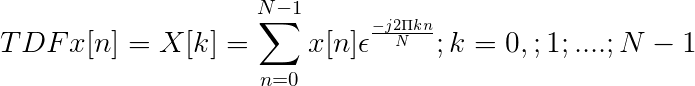
Luego de dada una secuencia discreta X[n]
La inversa de la transformada discreta de Fourier se define a través de la expresión:
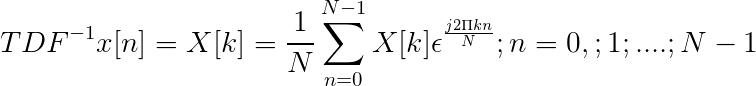
Permite una vez conseguida la transformada discreta, definir la secuencia en el dominio del tiempo X[n].
El proceso de parametrización correspondiente a la transformada discreta de Fourier radica en el enventanado. Para trabajar la transformada debemos limitar en tiempo a la secuencia. En muchos casos las señales en cuestión no cuentan con dichas limitaciones.
Una sucesión que no cumple con los criterios de tamaño para aplicar a la transformada discreta, puede ser multiplicada por una función “ventana” V[n], definiendo el comportamiento de la sucesión en un parámetro controlado.
X[n] . V[n]
El ancho del espectro será dependiente del ancho de la ventana. A medida que el ancho de la ventana aumente, la transformada calculada será más estrecha.
La transformada discreta de Fourier es una potente herramienta en el estudio de sucesiones discretas.
La transformada discreta de Fourier transforma una función variable continua, en una transformada de variable discreta.
El problema de Cauchy para la ecuación del calor presenta un campo de aplicación frecuente de la transformada discreta de Fourier. Donde se genera la función núcleo de calor o núcleo de Dirichlet, la cual aplica para muestreos de valores en un parámetro definido.
El motivo general de la aplicación de la transformada discreta de Fourier en esta rama se debe mayormente a la descomposición característica de una señal como superposición infinita de señales más fácilmente tratables.
Puede tratarse de una onda de sonido o una onda electromagnética, la transformada discreta de Fourier la expresa en una superposición de ondas simples. Esta representación es bastante frecuente en ingeniería eléctrica.
Son series definidas en términos de Cosenos y Senos. Sirven para facilitar el trabajo con funciones periódicas generales. Al aplicarse forman parte de las técnicas de resolución de ecuaciones diferenciales parciales y ordinarias.
Las series de Fourier son incluso más generales que las series de Taylor, debido a que desarrollan funciones discontinuas periódicas que no tienen representación en series de Taylor.
Para comprender analíticamente la transformada de Fourier es importante revisar las otras formas en las que se puede encontrar a la serie de Fourier, hasta poder definir la serie de Fourier en su notación compleja.
-Serie de Fourier sobre una función de periodo 2L:
Muchas veces es necesario adaptar la estructura de una serie de Fourier, a funciones periódicas cuyo periodo sea p = 2L > 0 en el intervalo [ -L , L ].
-Series de Fourier en funciones pares e impares
Se considera el intervalo[ –π , π ] el cual ofrece ventajas a la hora de aprovechar las características simétricas de las funciones.
Si f es par se establece la serie de Fourier como una serie de Cosenos.
Si f es impar se establece la serie de Fourier como una serie de Senos.
-Notación compleja de la serie de Fourier
Si se tiene una función f (t), que cumple con todos los requerimientos de la serie de Fourier, es posible denotarla en el intervalo [ -t , t ] utilizando su notación compleja:
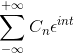
Con respecto al cálculo de la solución fundamental se presentan los siguientes ejemplos:
Ecuación de Laplace
Ecuación del calor
Ecuación de Schrödinger
Ecuación de ondas
Por otra parte, son ejemplos de aplicación de la transformada discreta de Fourier en el ámbito de la teoría de la señal los siguientes:
-Problemas de identificación del sistema. Establecidas f y g
-Problema con la consistencia de la señal de salida
-Problemas con el filtraje de la señal
Calcular la transformada discreta de Fourier para la siguiente sucesión.
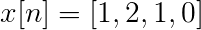
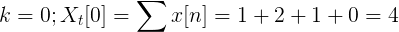
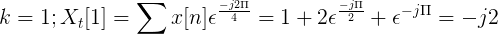
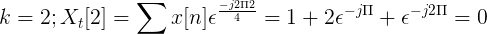
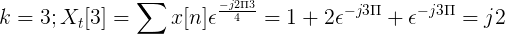
Se puede definir la TDF de x[n] como:
Xt[k] = {4, -j2, 0 , j2} para k = 0, 1, 2, 3
Se quiere determinar a través de un algoritmo digital la señal espectral definida por la expresión x(t)=e-t. Donde la frecuencia máxima que solicita coeficiente es fm=1Hz. Corresponde un armónico a f=0.3 Hz. El error se acota a menos del 5%. Calcular fs , D y N.
Tomando en cuenta el teorema del muestreo fs = 2fm = 2 Hz
Se escoge una resolución frecuencial de f0 = 0.1 Hz, de donde se obtiene D = 1/0,1 = 10s
0.3 Hz es la frecuencia correspondiente al índice k = 3, donde N = 3×8 = 24 muestreos. Indicando que fs = N/D = 24/10 = 2.4 > 2
Debido a que la finalidad es conseguir el menor valor posible para N, se pueden considerar los siguientes valores como solución:
f0 = 0.3 Hz
D = 1/0.3 = 3.33s
k = 1
N = 1×8 = 8
- Mastering the Discrete Fourier Transform in One, Two or Several Dimensions: Pitfalls and Artifacts. Isaac Amidror. Springer Science & Business Media, 19 jul. 2013
- The DFT: An Owners’ Manual for the Discrete Fourier Transform. William L. Briggs, Van Emden Henson. SIAM, 1 ene. 1995
- Digital Signal Processing: Theory and Practice. D. Sundararajan. World Scientific, 2003
- Transforms and Fast Algorithms for Signal Analysis and Representations. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6 dic. 2012
- Discrete and Continuous Fourier Transforms: Analysis, Applications and Fast Algorithms. Eleanor Chu. CRC Press, 19 mar. 2008
