Transformada de Laplace: qué es, definición, historia, propiedades

¿Qué es la transformada de Laplace?

La transformada de Laplace ha sido en los últimos años de gran importancia en los estudios de ingeniería, matemática, física, entre otras áreas científicas, ya que además de ser de gran interés en lo teórico, proporciona una forma sencilla de resolver ecuaciones diferenciales, transformándolas en ecuaciones algebraicas.

Originalmente la transformada de Laplace fue presentada por Pierre-Simon Laplace (1745-1827) en su estudio sobre la teoría de la probabilidad, y en principio fue tratada como un objeto matemático de interés meramente teórico.

Las aplicaciones actuales surgen cuando diversos matemáticos trataron de dar una justificación formal a las “reglas operacionales” usadas por Oliver Heaviside (1850-1925) en el estudio de ecuaciones de la teoría electromagnética.

Definición de la transformada de Laplace

Sea f una función definida para t ≥ 0. La transformada de Laplace se define como sigue:

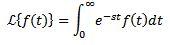
Se dice que la transformada de Laplace existe si la integral anterior converge, en caso contrario se dice que la transformada de Laplace no existe.

Por lo general, para denotar la función que se desea trasformar se usan letras minúsculas y la letra mayúscula corresponde a su transformada. De esta manera tendremos:

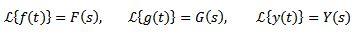
Ejemplos

Considere la función constante f(t) = 1. Tenemos que su transformada es:

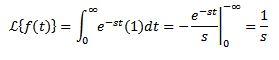
Siempre que la integral converja, es decir, siempre que s > 0. En caso contrario, s 0, la integral diverge.

Sea g(t)=t. Su transformada de Laplace viene dada por:

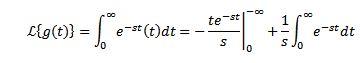
Al integrar por partes y sabiendo que te^-st tiende a 0 cuando t tiende a infinito y s > 0, junto con el ejemplo anterior tenemos que:

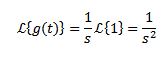
La transformada puede o no existir, por ejemplo para la función f(t) = 1/t, la integral que define su transformada de Laplace no converge y por lo tanto su transformada no existe.

Las condiciones suficientes para garantizar que la transformada de Laplace de una función f exista, son que f sea continua por partes para t ≥ 0 y sea de orden exponencial.

Se dice que una función es continua por partes para t ≥ 0, cuando para cualquier intervalo [a, b] con a > 0, hay un número finito de puntos t_k, en donde f tiene discontinuidades y es continua en cada subintervalo [t_k-1,t_k].

Por otro lado, se dice que una función es de orden exponencial c si existen constantes reales M > 0, c y T > 0 tal que:

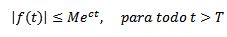
Como ejemplos tenemos que f(t) = t² es de orden exponencial, ya que |t²| e^3t para todo t > 0.

De manera formal tenemos el siguiente teorema:

Teorema (Condiciones suficientes para la existencia)

Si f es una función continua por parte para t > 0 y de orden exponencial c, entonces existe la transformada de Laplace para s > c.

Es importante resaltar que esta es una condición de suficiencia, es decir, que podría darse el caso de que exista una función que no cumpla dichas condiciones y aun así su transformada de Laplace exista.

Un ejemplo de esto es la función f(t) = t^-1/2 que no es continua por partes para t ≥ 0 pero su transformada de Laplace existe.

Transformada de Laplace de algunas funciones básicas

En la siguiente tabla se muestran las transformadas de Laplace de las funciones más comunes.

Historia de la transformada de Laplace

La transformada de Laplace debe su nombre a Pierre-Simon Laplace, matemático, y astrónomo y teórico francés que nació en 1749 y murió en 1827. Su fama era tal que fue conocido como el Newton de Francia.

En 1744, Leonard Euler (1707-1783) dedicó sus estudios a integrales con la forma

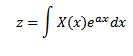
como soluciones de ecuaciones diferenciales ordinarias, pero rápidamente abandonó esta investigación. Más adelante, Joseph Louis Lagrange (1736-1813), quien admiraba mucho a Euler, también investigó este tipo de integrales y las relacionó con la teoría de la probabilidad.

1782, Laplace

En 1782 Laplace comenzó a estudiar dichas integrales como soluciones a ecuaciones diferenciales y, según los historiadores, en 1785 decidió reformular el problema, lo que luego dio nacimiento a las transformadas de Laplace tal y como hoy se entienden.

Al haber sido introducidas en el campo de la teoría de la probabilidad, fue de poco interés para los científicos del momento, y solo fue vista como un objeto matemático únicamente de interés teórico.

Oliver Heaviside

Fue a mediados del siglo XIX cuando el ingeniero inglés Oliver Heaviside descubrió que los operadores diferenciales pueden ser tratados como variables algebraicas, dándole así su moderna aplicación a las transformadas de Laplace.

Oliver Heaviside fue un físico, ingeniero eléctrico y matemático inglés que nació en 1850 en Londres y murió en 1925. Mientras intentaba resolver problemas de ecuaciones diferenciales aplicadas a la teoría de vibraciones, y usando los estudios de Laplace, empezó a dar forma a las aplicaciones modernas de las transformadas de Laplace.

Los resultados expuestos por Heaviside se esparcieron rápidamente por toda la comunidad científica de la época, pero al ser su trabajo poco riguroso fue rápidamente criticado por los matemáticos más tradicionales.

No obstante, la utilidad del trabajo de Heaviside a la hora de resolver ecuaciones de la física hizo que sus métodos fueran populares entre físicos e ingenieros.

A pesar de estos contratiempos y después de algunas décadas de intentos fallidos, a principios del siglo XX se le pudo dar una justificación rigurosa a las reglas operacionales establecidas por Heaviside.

Estos intentos dieron sus frutos gracias a los esfuerzos de diversos matemáticos, como Bromwich, Carson, Van der Pol, entre otros.

Propiedades de la transformada de Laplace

Entre las propiedades de la transformada de Laplace destacan las siguientes:

Linealidad

Sean c1 y c2 constantes y f(t) y g(t) funciones cuyas transformadas de Laplace son F(s) y G(s) respectivamente, entonces se tiene que:

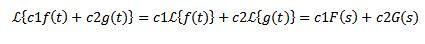
Debido a esta propiedad se dice que la transformada de Laplace es un operador lineal.

Ejemplo:

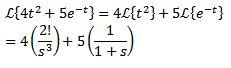
Primer teorema de traslación

Si ocurre que:

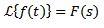
Y ‘a’ es cualquier número real, entonces:

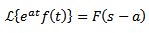
Ejemplo:

Como la transformada de Laplace de cos(2t) = s/(s^2 + 4) entonces:

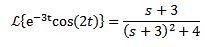
Segundo teorema de traslación

Si

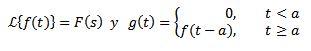
Entonces

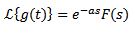
Ejemplo:

Si f(t) = t^3 , entonces F(s) = 6/s^4. Y por lo tanto, la transformada de 

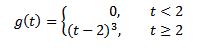
es G(s)= 6e^-2s/s^4

Cambio de escala

Si

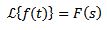
Y ‘a’ es un real distinto de cero, tenemos que

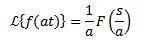
Ejemplo:

Como la transformada de f(t)= sen(t) es F(s)= 1/(s^2 + 1) se tiene que

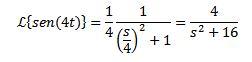
Transformada de Laplace de las derivadas

Si f, f’, f’’,…, f⁽ⁿ⁾ son continuas para t ≥ 0 y son de orden exponencial y f⁽ⁿ⁾(t) es continua por partes para t ≥ 0, entonces

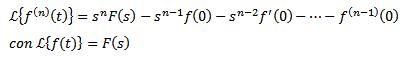
Transformada de Laplace de integrales

Si

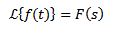
Entonces

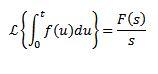
Multiplicación por tⁿ

Si tenemos que

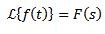
Entonces

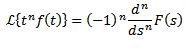
División por t

Si tenemos que

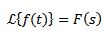
Entonces

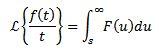
Funciones periódicas

Sea f una función periódica con periodo T > 0, es decir, f(t +T) = f(t), entonces

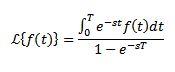
Comportamiento de F(s) cuando s tiende a infinito

Si f es continua por partes y de orden exponencial y

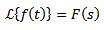
Entonces

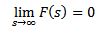
Transformadas inversas

Cuando aplicamos la transformada de Laplace a una función f(t) obtenemos F(s), la cual representa dicha transformada. De igual manera podemos decir que f(t) es la transformada de Laplace inversa de F(s), y se escribe como

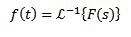
Sabemos que las transformadas de Laplace de f(t) = 1 y g(t) = t son F(s) = 1/s y G(s) = 1/s² respectivamente, por lo tanto tenemos que

Algunas transformadas de Laplace inversas comunes son las siguientes

Además, la transformada de Laplace inversa es lineal, es decir, se cumple que

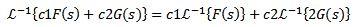
Ejercicio

Encuentre

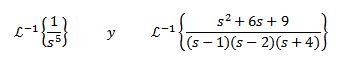
Para resolver este ejercicio debemos hacer coincidir la función F(s) con alguna de la tabla anterior. En este caso, si tomamos a n + 1 = 5 y usando la propiedad de linealidad de la transformada inversa, multiplicamos y dividimos por 4! Obteniendo

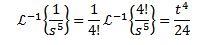
Para la segunda transformada inversa aplicamos fracciones parciales para reescribir la función F(s) y luego la propiedad de la linealidad, obteniendo

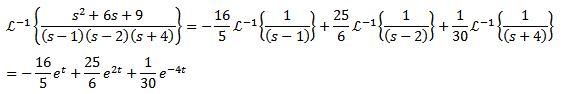
Como podemos observar de estos ejemplos, es común que la función F(s) que se evalúa no concuerde precisamente con alguna de las funciones dadas en la tabla. Para estos casos, como se observa, basta con reescribir la función hasta llegar a la forma adecuada.

Aplicaciones de la transformada de Laplace

Ecuaciones diferenciales

La principal aplicación que poseen las transformadas de Laplace es para resolver ecuaciones diferenciales.

Usando la propiedad de la transformada de una derivada es claro que

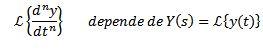
Y de las n-1 derivadas evaluadas en t = 0.

Esta propiedad hace que la transformada sea de gran utilidad para la resolución de problemas de valores iniciales donde estén involucradas ecuaciones diferenciales con coeficientes constantes.

Los siguientes ejemplos muestran cómo usar la transformada de Laplace para resolver ecuaciones diferenciales.

Ejemplo 1

Dado el siguiente problema de valor inicial

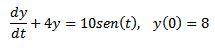
Use la transformada de Laplace para encontrar la solución.

Aplicamos la transformada de Laplace a cada miembro de la ecuación diferencial

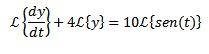
Por la propiedad de la transformada de una derivada tenemos

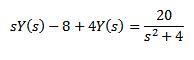
Al desarrollar toda la expresión y despejar Y(s) nos queda

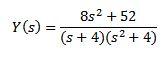
Usando fracciones parciales para reescribir el lado derecho de la ecuación obtenemos

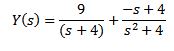
Finalmente, nuestro objetivo es encontrar una función y(t) que satisfaga la ecuación diferencial. Usando la transformada de Laplace inversa nos da como resultado

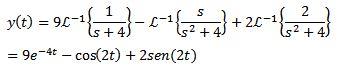
Ejemplo 2

Resuelva

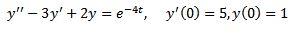
Como en el caso anterior, aplicamos la transformada en ambos lados de la ecuación y separamos término a término.

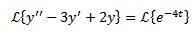
De esta manera tenemos como resultado

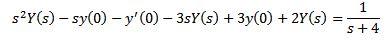
Sustituyendo con los valores iniciales dados y despejando Y(s)

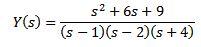
Usando fracciones simples podemos reescribir como sigue la ecuación

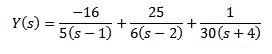
Y aplicando la transformada inversa de Laplace nos da como resultado

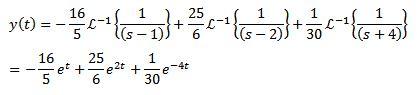
En estos ejemplos se podría llegar a la conclusión equivocada de que este método no es mucho mejor que los métodos tradicionales para resolver ecuaciones diferenciales.

Las ventajas que ofrece la transformada de Laplace es que no es necesario usar variación de parámetros o preocuparse por los diversos casos del método de coeficientes indeterminados.

Además, al resolver problemas de valor inicial por este método, desde el principio usamos las condiciones iniciales, por lo que no es necesario realizar otros cálculos para encontrar la solución particular.

Sistemas de ecuaciones diferenciales

La transformada de Laplace también puede ser utilizada para encontrar soluciones a ecuaciones diferenciales ordinarias simultáneas, como muestra el siguiente ejemplo.

Ejemplo

Resolver

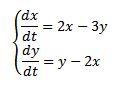
Con las condiciones iniciales x(0) = 8 e y(0) = 3.

Si tenemos que

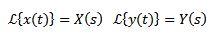
Entonces

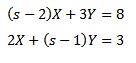
Resolviendo nos da como resultado

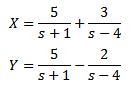
Y al aplicar la transformada inversa de Laplace tenemos

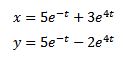
Mecánica y circuitos eléctricos

La transformada de Laplace es de gran importancia en la física, principalmente tiene aplicaciones para la mecánica y los circuitos eléctricos.

Un circuito eléctrico simple está compuesto de los siguientes elementos:

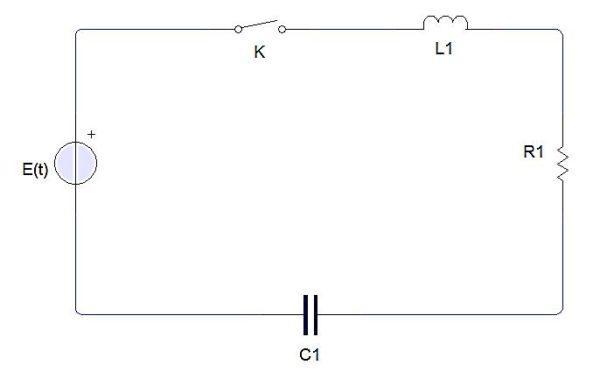
Un interruptor, una batería o fuente, un inductor, una resistencia y un capacitor. Cuando el interruptor es cerrado se produce una corriente eléctrica que se denota por i(t). La carga del capacitor se denota por q(t).

Por la segunda ley de Kirchhoff el voltaje producido por la fuente E al circuito cerrado tiene que ser igual a la suma de cada una de las caídas de voltaje.

La corriente eléctrica i(t) se relaciona con la carga q(t) en el capacitor mediante i = dq/dt. Por otro lado, se define la caída de voltaje en cada uno de los elementos como sigue:

La caída de voltaje en una resistencia es iR = R(dq/dt)

La caída de voltaje en un inductor es L (di/dt) = L(d²q/dt²)

La caída de voltaje en un capacitor es  q/C

Con estos datos, y aplicando la segunda ley de Kirchhoff al circuito simple cerrado, se obtiene una ecuación diferencial de segundo orden que describe el sistema y nos permite determinar el valor de q(t).

Ejemplo

Un inductor, un capacitor y una resistencia se conectan a una batería E, como se muestra en la figura. El inductor es de 2 henries, el capacitor de 0,02 farads y la resistencia de 16 onhmios. En el instante t = 0 se cierra el circuito. Encontrar la carga y la corriente en cualquier tiempo t > 0 si E = 300 voltios.

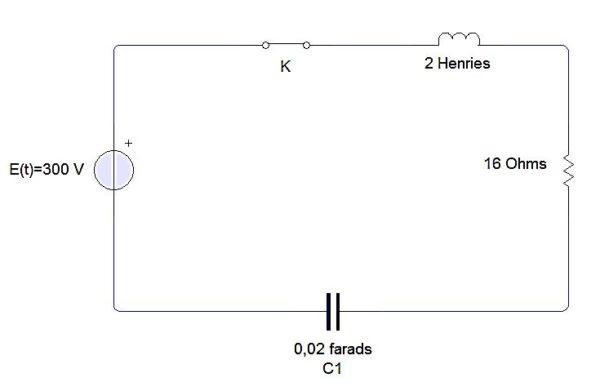
Tenemos que la ecuación diferencial que describe este circuito es la siguiente:

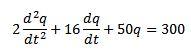
Donde las condiciones iniciales son q(0) =  0, i(0) = 0 = q’(0).

Aplicando la transformada de Laplace conseguimos que

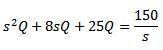
Y despejando Q(t)

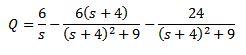
Luego, aplicando la transformada inversa de Laplace tenemos

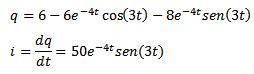
Referencias

1. G.Holbrook, J. (1987). Transformada de Laplace para ingenieros en electrónica. Limusa.
2. Ruiz, L. M., & Hernandez, M. P. (2006). Ecuaciones diferenciales y transformada de Laplace con aplicaciones. Editorial UPV.
3. Simmons, G. F. (1993). Ecuaciones diferenciales con aplicaciones y notas históricas. McGraw-Hill.
4. Spiegel, M. R. (1991). Transformadas de Laplace. McGraw-Hill.
5. Zill, D. G., & Cullen, M. R. (2008). Ecuaciones diferenciales con problemas de valores en la frontera. Cengage Learning Editores, S.A.