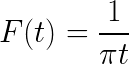Transformada de Fourier: propiedades, aplicaciones, ejemplos

La transformada de Fourier es un método de adecuación analítica orientado a funciones integrables que pertenece a la familia de las transformadas integrales. Consiste en una redefinición de funciones f (t) en términos de Cos (t) y Sen (t).

Las identidades trigonométricas de dichas funciones, en conjunto con sus características de derivación y antiderivación, sirven para definir la transformada de Fourier a través de la siguiente función compleja:

Lo cual se cumple mientras la expresión tenga sentido, es decir cuando la integral impropia sea convergente. Algebraicamente se dice que la transformada de Fourier  es un homeomorfismo lineal.

Toda función que pueda ser trabajada con transformada de Fourier debe presentar nulidad fuera de un parámetro definido.

Índice del artículo

• 1 Propiedades
  • 1.1 Existencia
  • 1.2 Linealidad de la transformación de Fourier
  • 1.3 Transformada de Fourier de una derivada
  • 1.4 Diferenciación de la transformada de Fourier
  • 1.5 Transformada de Fourier de una traslación
  • 1.6 Traslación de la transformada de Fourier
  • 1.7 Transformada de Fourier de un grupo de escala
  • 1.8 Simetría
  • 1.9 Transformada de Fourier de un producto en convolución
  • 1.10 Continuidad y caída en infinito
• 2 Historia
• 3 ¿Para qué sirve la transformada de Fourier?
  • 3.1 La serie de Fourier
  • 3.2 Otras formas de la serie de Fourier
• 4 Aplicaciones
  • 4.1 Cálculo de la solución fundamental
  • 4.2 Teoría de la señal
• 5 Ejemplos
  • 5.1 Ejemplo 1
  • 5.2 Ejemplo 2
• 6 Ejercicios propuestos
• 7 Referencias

Propiedades

La transformada de Fourier cumple con las siguientes propiedades:

Existencia

Para verificar la existencia de la transformada de Fourier en una función f (t) definida en los reales R, se deben cumplir los siguientes 2 axiomas:

1. f (t) es continua a trozos para todo R
2. f (t) es integrable en R

Linealidad de la transformación de Fourier

Sean M (t) y N (t) dos funciones cualesquiera con transformadas de Fourier definidas, con constantes a y b cualquiera.

F [ a M(t) + b N(t) ] (z) = a F [ M(t) ] (z) + b F [ N(t) ] (z)

Lo cual se apoya también en la linealidad de la integral del mismo nombre.

Transformada de Fourier de una derivada

Se tiene una función f  que es continua e integrable en todos los reales, donde:

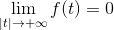
Y la derivada de f ( f’ ) es continua y definida a trozos en todo R

La transformada de Fourier de una derivada queda definida mediante la integración por partes, por la siguiente expresión:

F [ f’ (t) ] (z) = izF [ f (t) ] (z)

En las derivaciones de orden superior, se aplicará de manera homóloga, donde para toda n  1 se tiene que:

F [ f ⁿ’ (t) ] (z) = (iz)ⁿF [ f (t) ] (z)

Diferenciación de la transformada de Fourier

Se tiene una función f  que es continua e integrable en todos los reales, donde:

i (d/dz) F [ f (t) ] (z) = F  [t .  f (t) ] (z)

Transformada de Fourier de una traslación

Para todo θ que pertenece a un conjunto S y T que pertenece al conjunto S’, se tiene que:

F [ τ_aθ ] =  e^-iayF [ θ ]                                 F [ τ_aT ] =  e^-iax  F [ T ]   

Con  τ_a  trabajando como el operador de traslación sobre el vector a.

Traslación de la transformada de Fourier

Para todo θ que pertenece a un conjunto S y T que pertenece al conjunto S’, se tiene que:

τ_a F [ θ ] =  F [e^-iax.θ ]                                τ_a F [T ] =  F [e^-iay. T ]

Para todo a que pertenece a R

Transformada de Fourier de un grupo de escala

Para todo θ que pertenece a un conjunto S. T que pertenece al conjunto S’

λ perteneciente a R – { 0 }  se tiene que:

F [ θ ( λx ) ] = ( 1 / |λ| ) F [ θ ] (y/λ)                 

 F [ T ( λx ) ] = ( 1 / |λ| ) F [ T ] (y/λ)

Si f es una función continua y netamente integrable, donde a > 0. Entonces:

F [ f ( at) ] (z) =   (1/a) F [ f ( t ) ] (z/a)   

Para demostrar este resultado se puede proceder con el cambio de variable.

Cuando T → +  entonces s = at → +∞

Cuando T → –  entonces s = at → – ∞

Simetría

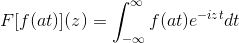
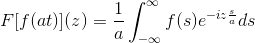
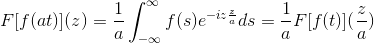
Para estudiar la simetria de la transformada de Fourier se deben verificar la identidad de Parseval y la fórmula de Plancherel.

Se tiene θ y δ que pertenecen a S. Desde allí puede deducirse que:

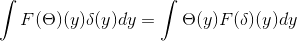
Obteniéndose

1 / (2π)^d  { F [ θ ] , F [δ ] }     Identidad de Parseval

1 / (2π)^d/2  || F [ θ ] ||_L²_R^d     fórmula de Plancherel

Transformada de Fourier de un producto en convolución

Persiguiendo objetivos similares que en la transformada de Laplace, la convolución de funciones se refiere al producto entre sus transformadas de Fourier.

Se tiene f y g como 2 funciones acotadas, definidas y completamente integrables:

F ( f *g ) = F ( f ) . F ( g )

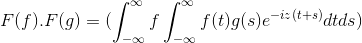
Luego al efectuar el cambio de variable

t + s = x ; se continua con la doble integral impropia

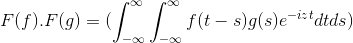
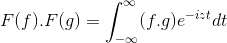
F (f) . F (g) = F ( f . g )

Continuidad y caída en infinito

Para todo θ que pertenece a R, F [ θ ] obedece a los criterios de función continua acotada en R^d.

También { F [ θ ]( y ) } → 0 en C si |y| → ∞

Historia

Este concepto matemático fue presentado por Joseph B. Fourier en el año 1811 mientras desarrollaba un tratado referente a la propagación de calor. Rápidamente fue adoptado por diversas ramas de la ciencia e ingeniería.

Se estableció como principal herramienta de trabajo en el estudio de las ecuaciones con derivadas parciales, comparándose incluso con la relación de trabajo existente entre la transformada de Laplace y las ecuaciones diferenciales ordinarias.

¿Para qué sirve la transformada de Fourier?

Sirve principalmente para simplificar de manera notable las ecuaciones, mientras transforma expresiones derivadas en elementos de potencia, que denotan expresiones diferenciales en forma de polinomios integrables.

En la optimización, modulación y modelación de resultados actúa como expresión estandarizada, siendo un recurso frecuente para la ingeniería tras varias generaciones.

La serie de Fourier

Son series definidas en términos de Cosenos y Senos; sirven para facilitar el trabajo con funciones periódicas generales. Al aplicarse forman parte de las técnicas de resolución de ecuaciones diferenciales parciales y ordinarias.

Las series de Fourier son incluso más generales que las series de Taylor, debido a que desarrollan funciones discontinuas periódicas que no tienen representación en series de Taylor.

Otras formas de la serie de Fourier

Para comprender analíticamente la transformada de Fourier es importante revisar las otras formas que en las que se puede encontrar a la serie de Fourier, hasta poder definir la serie de Fourier en su notación compleja.

-Serie de Fourier sobre una función de periodo 2L

Muchas veces es necesario adaptar la estructura de una serie de Fourier, a funciones periódicas cuyo periodo sea    p = 2L > 0 en el intervalo [ -L , L ].

-Series de Fourier en funciones pares e impares

Se considera el intervalo[ –π , π ] el cual ofrece ventajas a la hora de aprovechar las características simétricas de las funciones.

Si f es par se establece la serie de Fourier como una serie de Cosenos.

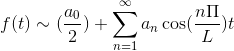
Si f es impar se establece la serie de Fourier como una serie de Senos.

-Notación compleja de la serie de Fourier

Si se tiene una función f (t), que cumple con todos los requerimientos de desarrollabilidad de la serie de Fourier, es posible denotarla en el intervalo [ -t , t ] utilizando su notación compleja:

Aplicaciones

Cálculo de la solución fundamental

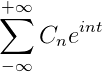
La transformada de Fourier es una potente herramienta en el estudio de ecuaciones diferenciales parciales del tipo lineal con coeficientes constantes. Aplican para funciones con dominios no acotados por igual.

Al igual que la transformada de Laplace, la transformada de Fourier transforma una función de derivadas parciales, en una ecuación diferencial ordinaria mucho más sencilla de operar.

El problema de Cauchy para la ecuación del calor presenta un campo de aplicación frecuente de la transformada de Fourier donde se genera la función núcleo de calor o núcleo de Dirichlet.

Con respecto al cálculo de la solución fundamental se presentan los siguientes casos donde es común encontrar la transformada de Fourier:

-Ecuación de Laplace

-Ecuación del calor

-Ecuación de Schrödinger

-Ecuación de ondas

Teoría de la señal

El motivo general de la aplicación de la transformada de Fourier en esta rama se debe mayormente a la descomposición característica de una señal como superposición infinita de señales más fácilmente tratables.

Puede tratarse de una onda de sonido o una onda electromagnética, la transformada de Fourier la expresa en una superposición de ondas simples. Esta representación es bastante frecuente en ingeniería eléctrica.

Por otra parte, son ejemplos de aplicación de la transformada de Fourier en el ámbito de la teoría de la señal:

-Problemas de identificación del sistema. Establecidas f y g

-Problema con la consistencia de la señal de salida

-Problemas con el filtraje de la señal

Ejemplos

Ejemplo 1

Definir la transformada de Fourier para la siguiente expresión:

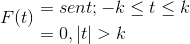
También podemos representarlo de la siguiente forma:

F (t) = Sen ( t ) [ H_{( t + k )} – H_{( t – k)} ]

Se define el pulso rectangular:

p (t) =  H_{( t + k )} – H_{( t – k)}

Se aplica la transformada de Fourier a la siguiente expresión que se asemeja al teorema de modulación.

f (t) =p (t) Sen (t)

Donde: F [ w ] = (1/2) i [ p (w + 1) – p (w – 1) ]

Y la transformada de Fourier queda definida por:

F [ w ] =  (1/2) i [ (2/2w+1) Sen ( k(w+1) ) – (2/2w+1) Sen ( k(w-1) ) ]

Ejemplo 2

Definir la transformada de Fourier para la expresión:

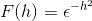
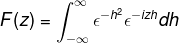
Debido a que f(h) es una función par, se puede afirmar que

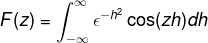
Se aplica integración por partes seleccionando las variables y sus diferenciales de la siguiente manera

u = sen (zh)                    du= z cos (zh) dh

dv = h (e^-h)²                       v = (e^-h)² / 2

Sustituyendo se tiene

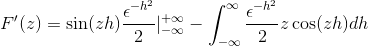
Tras evaluar bajo el teorema fundamental del cálculo

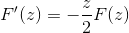
Aplicando conocimientos previos referentes a las ecuaciones diferenciales de primer orden, la expresión se denota como

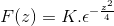
Para obtener K evaluamos 

Por último se define la transformada de Fourier de la expresión como

Ejercicios propuestos

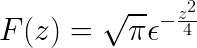
• Consiga la transformada de la expresión W/(1+w²)

Referencias

1. Duoandikoetxea Zuazo, J., Análisis de Fourier. Addison– Wesley Iberoamericana, Universidad Autónoma de Madrid, 1995.
2. Lions, J. L., Mathematical Analysis and Numerical Methods for Science and Technology. Springer–Verlag, 1990.
3. Lieb, E. H., Gaussian kernels have only gaussian maximizers. Invent. Math. 102, 179–208, 1990.
4. Dym, H., McKean, H. P., Fourier Series and Integrals. Academic Press, Nueva York, 1972.
5. Schwartz, L., Théorie des Distributions. Ed. Hermann, París, 1966.