Arco (geometría): medida, tipos de arcos, ejemplos
El arco, en geometría, es toda línea curva que conecta dos puntos. Una línea curva, a diferencia de una línea recta, es aquella cuya dirección es diferente en cada punto de la misma. Lo contrario de un arco es un segmento, ya que este es un tramo recto que une dos puntos.
El arco que más frecuentemente se usa en geometría es el arco de circunferencia. Otros arcos de uso común son el arco parabólico, arco elíptico y el arco catenario. La forma de arco también se utiliza frecuentemente en arquitectura como elemento decorativo y elemento estructural. Es el caso de los dinteles de las puertas y ventanas, así como de los puentes y acueductos.

Índice del artículo
La medida de un arco es su longitud, la cual depende del tipo de curva que conecta los dos puntos y de la ubicación de los mismos.
La longitud de un arco circular es una de las más sencillas de calcular, debido a que se conoce la longitud del arco completo o perímetro de una circunferencia.
El perímetro de una circunferencia es dos pi veces su radio: p = 2 π R. Sabiendo esto, si se quiere calcular la longitud s de un arco circular de ángulo α (medido en radianes) y radio R, se aplica una proporción:
(s / p) = ( α / 2 π )
Luego, despejando s de la expresión anterior y sustituyendo el perímetro p por su expresión en función del radio R, se tiene:
s = ( α / 2 π ) p = ( α / 2 π ) (2 π R) = α R.
Es decir, que la medida de un arco circular es el producto de su apertura angular por el radio del arco circular.
Para un arco de forma general el problema es más complicado, al punto que los grandes pensadores de la antigüedad afirmaban que era una tarea imposible.
No fue sino hasta el advenimiento del cálculo diferencial e integral en 1665, que el problema de la medida de un arco cualquiera se resolvió satisfactoriamente.
Antes de la invención del cálculo diferencial solo se podían encontrar soluciones mediante el uso de línea poligonales o arcos de circunferencia que aproximaban al arco verdadero, pero estas soluciones no eran exactas.
Desde el punto de vista de la geometría, los arcos se clasifican según la línea curva que une dos puntos del plano. Hay otras clasificaciones de acuerdo a su uso y forma arquitectónica.
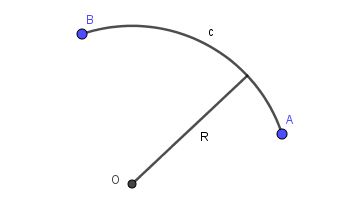
Cuando la línea que conecta dos puntos del plano es un trozo de circunferencia de cierto radio, se tiene un arco circular. La figura 2 muestra un arco circular c de radio R que conecta los puntos A y B.
La parábola es la trayectoria que sigue un objeto que se ha lanzado al aire en forma oblicua. Cuando la curva que une dos puntos es una parábola, entonces se tiene un arco parabólico como el mostrado en la figura 3.
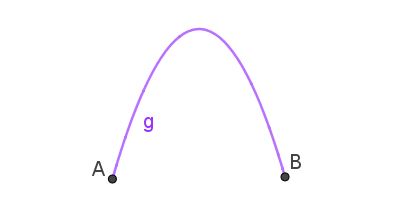
Esta es la forma que adopta el chorro de agua que sale de una manguera que se apunta hacia arriba. El arco parabólico puede ser observado en la fuentes de agua.

El arco catenario es otro arco natural. La catenaria es la curva que se forma naturalmente cuando una cadena o una cuerda cuelga holgadamente desde dos puntos separados.
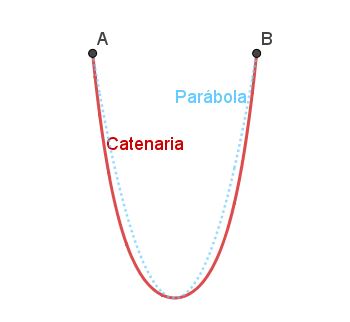
La catenaria es similar a la parábola, pero no es exactamente igual como puede notarse en la figura 4.
El arco en forma de catenaria invertida se usa en arquitectura como un elemento estructural de alta resistencia a la compresión. De hecho, puede demostrarse que es el tipo de arco más resistente entre todas las formas posibles.
Para construir un sólido arco catenario, solo se copia la forma de una cuerda o cadena colgando, luego la forma copiada se voltea para reproducirla en el dintel de la puerta o la ventana.
Un arco es elíptico si la curva que conecta dos puntos es un trozo o tramo de elipse. La elipse se define como el lugar geométrico de los puntos cuya distancia a dos puntos dados suma siempre una cantidad constante.
La elipse es una curva que aparece en la naturaleza: es la curva de la trayectoria de los planetas en torno al Sol, tal como lo demostró Johannes Kepler en el año 1609.
En la práctica una elipse puede dibujarse fijando dos puntales en el suelo o dos alfileres en un papel y atando una cuerda a los mismos. Luego se tensa la cuerda con el marcador o lápiz y se traza la curva. Un trozo de elipse es un arco elíptico. La siguiente animación ilustra cómo se traza la elipse:
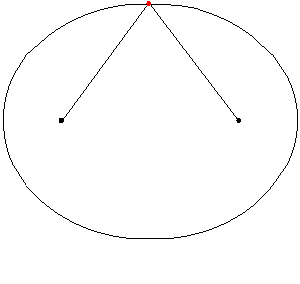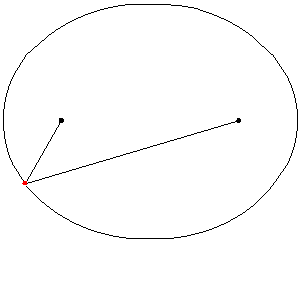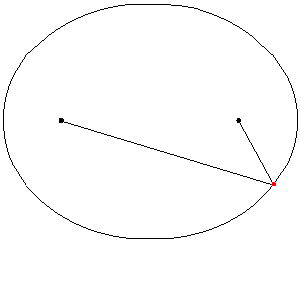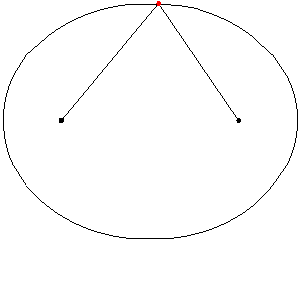
La figura 6 muestra un arco elíptico que conecta los puntos G y H.
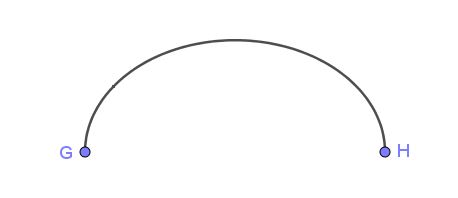
Los siguiente ejemplos se refieren a cómo calcular el perímetro de algunos arcos específicos.
La figura 7 muestra una ventana terminada en arco circular recortado. Las dimensiones mostradas en la figura están en pies. Calcule la longitud del arco.
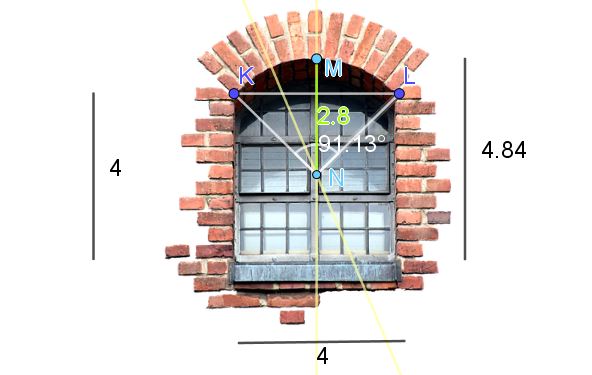
Para conseguir el centro y el radio del arco circular del dintel de la ventana se hacen las siguientes construcciones sobre la imagen:
-Se traza el segmento KL y se traza su mediatriz.
-Después se ubica el punto más alto del dintel, el cual llamamos M. Seguidamente se considera el segmento KM y se traza su mediatriz.
La intercepción de las dos mediatrices es el punto N y también es el centro del arco circular.
-Ahora hay que medir la longitud del segmento NM, la cual coincide con el radio R del arco circular: R = 2.8 pies.
-Para saber la longitud del arco además del radio se necesita conocer el ángulo que forma el arco. El cual puede determinarse por dos métodos, o bien se mide con un transportador, o alternativamente se calcula usando trigonometría.
En el caso mostrado el ángulo que forma el arco es 91,13º, el cual debe convertirse a radianes:
91,13º = 91,13º * π / 180º = 1,59 radianes
Finalmente calculamos la longitud s del arco mediante la fórmula s = α R.
s = 1,59 * 2.8 pies = 4,45 pies
Hallar la longitud del arco elíptico mostrado en la figura 8, conocidos el semieje mayor r y el semieje menor s de la elipse.
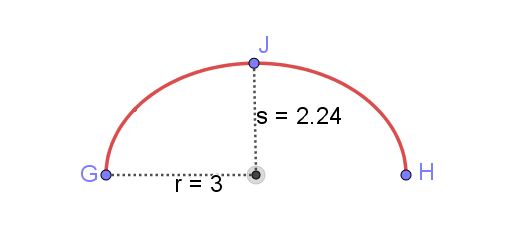
Hallar la longitud de una elipse fue por mucho tiempo uno de los problemas más difíciles de las matemáticas. Se pueden conseguir soluciones expresadas mediante integrales elípticas pero para tener un valor numérico hay que expandir dichas integrales en series de potencia. Un resultado exacto requeriría de infinitos términos de esas series.
Por fortuna, el genio matemático de origen hindú Ramanujan, quien vivió entre 1887 y 1920, encontró una fórmula que aproxima muy precisamente el perímetro de una elipse:
Perímetro de una elipse = π [ 3( r + s) – √((3r + s) (r +3s))]
El perímetro de una elipse con r = 3 cm y s = 2.24 cm es 16,55 cm. Sin embargo, el arco elíptico mostrado tiene la mitad de ese valor:
Longitud del arco elíptico GH = 8.28 cm.
- Clemens S. 2008. Geometría y Trigonometría. Pearson Education.
- García F. Procedimientos numéricos en Java. Longitud de una elipse. Recuperado de: sc.ehu.es
- Geometría dinámica. Arcos. Recuperado de geometriadinamica.es
- Piziadas. Elipses y parábolas a nuestro alrededor. Recuperado de: piziadas.com
- Wikipedia. Arco (geometría). Recobrado de: es.wikipedia.com
