Física

Dilatación superficial: fórmula, coeficientes y ejemplos

La dilatación superficial es la expansión que ocurre cuando un objeto experimenta variaciones de su superficie a causa de una variación de temperatura. Se debe a características propias del material o a su forma geométrica. La dilatación predomina en dos dimensiones en la misma proporción.

Por ejemplo en una lámina, cuando hay un variación de temperatura, es la superficie de la misma la que mayor cambio sufre a causa de la dilatación térmica.

La lámina metálica de la figura anterior aumenta su ancho y su largo de forma apreciable cuando es calentada por la radiación solar. Por el contrario, ambos disminuyen sensiblemente cuando es enfriada a causa de un descenso en la temperatura ambiente.

Es por esta razón que, cuando se instalan baldosas en un piso, no deben pegarse unos bordes con otros, sino que debe haber un espacio de separación denominado junta de dilatación.

Además ese espacio se llena con un mezcla especial que tiene cierto grado de flexibilidad, evitando que las baldosas se agrieten por las fuertes presiones que puede producir la dilatación térmica.

Índice del artículo

¿En qué consiste la dilatación superficial?

En un material sólido los átomos mantienen sus posiciones relativas más o menos fijas alrededor de un punto de equilibrio. Sin embargo, debido a la agitación térmica, siempre están oscilando en torno al mismo.

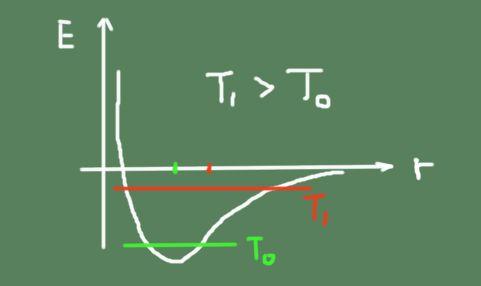
Al aumentar la temperatura, también aumenta la oscilación térmica, haciendo que las posiciones de oscilación media cambien. Esto es debido a que el potencial de enlace no es exactamente parabólico y tiene asimetría alrededor del mínimo.

A continuación se muestra una figura que esboza la energía de enlace químico en función de la distancia interatómica. Se muestra también la energía total de oscilación a dos temperaturas y cómo se desplaza el centro de oscilación.

Dilatación superficial y su coeficiente

Para medir la dilatación superficial partimos de un área inicial A y una temperatura inicial T, del objeto del cual se quiere medir la dilatación.

Supongamos que dicho objeto es una lámina de área A, y el espesor de la misma es mucho menor que la raíz cuadrada del área A. Se somete a la lámina a una variación de temperatura ΔT, de modo tal que la temperatura final de la misma una vez establecido el equilibrio térmico con la fuente de calor será T’=T+ ΔT.

Durante este proceso térmico, el área de la superficie también habrá cambiado a un nuevo valor A’ = A + ΔA, donde ΔA es la variación de la longitud. Así, se define el coeficiente de dilatación superficial σ como el cociente entre la variación relativa de área por unidad de variación de temperatura.

La siguiente fórmula define el coeficiente de dilatación superficial σ:

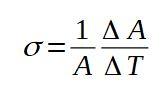
El coeficiente de dilatación superficial σ es prácticamente constante para un amplio rango de valores de temperatura.

Por la definición de σ sus dimensiones son inverso de temperatura. Como unidad se suele usar °C-1.

Coeficiente de dilatación superficial para varios materiales

A continuación daremos un listado del coeficiente de dilatación superficial para algunos materiales y elementos. El coeficiente está calculado a presión atmosférica normal en base a una temperatura ambiente de 25 °C, y su valor se considera constante en un rango de ΔT desde -10°C hasta 100 °C.

La unidad del coeficiente de dilatación superficial será (°C)-1

– Acero: σ = 24∙10-6 (°C)-1

– Aluminio: σ = 46∙10-6 (°C)-1

– Oro: σ = 28∙10-6 (°C)-1

– Cobre: σ = 34∙10-6 (°C)-1

– Latón: σ = 36∙10-6 (°C)-1

– Hierro: σ = 24∙10-6 (°C)-1

– Vidrio: σ = (14 a 18)∙10-6 (°C)-1

– Cuarzo: σ = 0,8∙10-6 (°C)-1

– Diamante: σ = 2,,4∙10-6 (°C)-1

– Plomo: σ = 60∙10-6 (°C)-1

– Madera de roble: σ = 108∙10-6 (°C)-1

– PVC: σ = 104∙10-6 (°C)-1

– Fibra de carbono: σ = -1,6∙10-6 (°C)-1

– Hormigón: σ = (16 a 24)∙10-6 (°C)-1

La mayoría de los materiales se estiran con un aumento de temperatura. Sin embargo, algunos materiales como la fibra de carbono se encojen con el aumento de temperatura.

Ejemplos resueltos de dilatación superficial

Ejemplo 1

Una placa de acero tiene unas dimensiones de 3m x 5m. En la mañana y a la sombra su temperatura es de 14 °C, pero al mediodía el Sol la calienta hasta los 52 °C. Encuentre el área final de la placa.

Solución

Partimos de la definición de coeficiente de dilatación superficial:

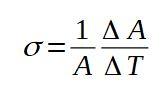
De acá despejamos la variación en el área:

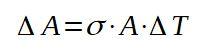
Procedemos entonces a sustituir los respectivos valores para encontrar el incremento de área por el aumento de la temperatura.

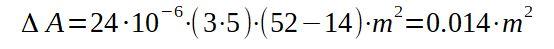
Es decir, que el área final será de 15,014 metros cuadrados.

Ejemplo 2

Demuestre que el coeficiente de dilatación superficial es aproximadamente el doble del coeficiente de dilatación lineal.

Solución

Supongamos que partimos de una placa rectangular de dimensiones ancho Lx y largo Ly, entonces su área inicial será A = Lx ∙ Ly

Cuando la placa sufre un incremento de temperatura ΔT, entonces sus dimensiones también se incrementan siendo su nuevo ancho Lx’ y su nuevo largo Ly’, de modo que su nueva área será A’ = Lx’ ∙ Ly’

La variación que sufrió el área de la placa por efecto del cambio de temperatura será entonces

ΔA = Lx’ ∙ Ly’ – Lx ∙ Ly

donde Lx’ = Lx ( 1 + α ΔT) y Ly’ = Ly ( 1 + α ΔT)

Es decir, que el cambio de área en función del coeficiente de dilatación lineal y el cambio de temperatura será:

ΔA = Lx ( 1 + α ΔT) ∙ Ly ( 1 + α ΔT) – Lx ∙ Ly

Este puede reescribirse como:

ΔA = Lx ∙ Ly ∙ ( 1 + α ΔT)² – Lx ∙ Ly

Desarrollando el cuadrado y multiplicando nos queda lo siguiente:

ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly+ (α ΔT)² Lx ∙ Ly – Lx ∙ Ly

Como α es del orden de 10-6, al elevarlo al cuadrado queda del orden de 10-12. Así, el término cuadrático en la expresión anterior es despreciable.

Entonces el incremento de área puede aproximarse por:

ΔA ≈ 2α ΔT Lx ∙ Ly

Pero el incremento de área en función del coeficiente de dilatación superficial es:

ΔA = γ ΔT A

De donde se deduce una expresión que relaciona el coeficiente de dilatación lineal con el coeficiente de dilatación superficial.

γ ≈ 2∙α

Referencias

  1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mac Graw Hill. 422-527
  2. Giancoli, D. 2006. Física: Principios con Aplicaciones. 6ta. Edition. Prentice Hall. 238–249.