Fuerza centrífuga: fórmulas, cómo se calcula, ejemplos, ejercicios
La fuerza centrífuga tiende a empujar hacia afuera a los cuerpos que giran tomando una curva. Se considera una fuerza ficticia, pseudofuerza o fuerza inercial, porque no es causada por interacciones entre objetos reales, sino que es una manifestación de la inercia de los cuerpos. La inercia es la propiedad que hace que los objetos quieran conservar su estado de reposo o de movimiento rectilíneo uniforme, si lo tienen.
El término “fuerza centrífuga” fue acuñado por el científico Christian Huygens (1629-1695). Él afirmaba que el movimiento curvilíneo de los planetas tendería a alejarlos a menos que el Sol ejerciera alguna fuerza para retenerlos y calculó que esta fuerza era proporcional al cuadrado de la velocidad e inversamente proporcional al radio del la circunferencia descrita.

Para quienes viajan en automóvil, la fuerza centrífuga no es ficticia en absoluto. Los pasajeros de un coche que gira a la derecha se sienten impulsados hacia la izquierda, y viceversa, cuando el coche gira a la izquierda, las personas experimentan una fuerza hacia la derecha, que parece querer alejarlos del centro de la curva.
La magnitud de la fuerza centrífuga Fgse calcula mediante la siguiente expresión:
–Fg es la magnitud de la fuerza centrífuga
–m es la masa del objeto
–v es la rapidez
–R es el radio de la trayectoria curva.
La fuerza es un vector, por lo tanto se usa letra negrita para distinguirla de su magnitud, que es un escalar.
Hay que tener muy presente siempre, que Fg aparece únicamente cuando se describe el movimiento usando un sistema de referencia acelerado.
En el ejemplo descrito al comienzo, el automóvil que gira constituye una referencia acelerada, ya que precisa de la aceleración centrípeta, para que pueda dar la vuelta.
Índice del artículo
La elección del sistema de referencia es vital para la apreciación del movimiento. Un sistema de referencia acelerado también se conoce como sistema no inercial.
En este tipo de sistema, como un auto que gira, aparecen fuerzas ficticias como la fuerza centrífuga, cuyo origen no es una interacción real entre objetos. Un pasajero no podría decir qué es lo que lo empuja fuera de la curva, solamente puede afirmar que ocurre así.
En cambio, en un sistema de referencia inercial, las interacciones se dan entre objetos reales, como por ejemplo el cuerpo en movimiento y la Tierra, que da lugar al peso, o entre el cuerpo y la superficie sobre la que se mueve, que originan rozamientos y normales.
Un observador parado al borde de la carretera y que ve al auto dar la curva, es un buen ejemplo de sistema de referencia inercial. Para este observador, el coche gira porque sobre él actúa una fuerza dirigida hacia el centro de la curva, que lo obliga a no salirse de ella. Se trata de la fuerza centrípeta producida por la fricción entre los neumáticos y el pavimento.
En un sistema de referencia inercial, la fuerza centrífuga no aparece. Por lo tanto el primer paso para la calcularla, es escoger cuidadosamente el sistema de referencia que se usará para describir el movimiento.
Finalmente, es preciso destacar que los sistemas de referencia inerciales no necesariamente deben estar en reposo, como el observador que mira al vehículo dar la curva. Un sistema de referencia inercial, conocido como marco de referencia del laboratorio, también puede estar en movimiento. Eso sí, con velocidad constante respecto a uno inercial.
En la siguiente figura a la izquierda, un observador O se encuentra de pie y mira a O’, quien se encuentra sobre la plataforma que gira en el sentido indicado. Para O, que es un marco inercial, ciertamente O’ se mantiene girando debido a la fuerza centrípeta Fc producida por la pared de la rejilla sobre la espalda del O’.
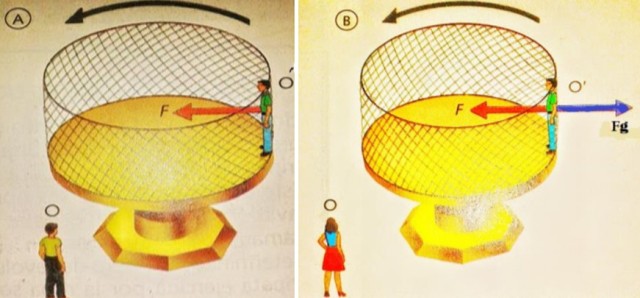
Únicamente en sistemas de referencia inerciales es válido aplicar la segunda Ley de Newton, la cual afirma que la fuerza neta equivale al producto de la masa por la aceleración. Y al hacerlo, con el diagrama de cuerpo libre mostrado, se obtiene:
Fc = mac
Fc= mv2 / R
Similarmente, en la figura de la derecha también hay un diagrama de cuerpo libre que describe lo que ve el observador O’. Desde su punto de vista, él está en reposo, por lo tanto las fuerzas sobre él se equilibran.
Estas fuerzas son: la normal F, que la pared ejerce sobre él, en rojo y dirigida hacia el centro y la fuerza centrífuga Fg que lo empuja hacia afuera y la cual no se origina por interacción alguna, es una fuerza no-inercial que aparece en los sistemas de referencia en rotación.
La fuerza centrífuga siendo ficticia, es equilibrada por una fuerza real, la fuerza de contacto o normal que apunta hacia el centro. Por lo tanto:
∑Fx = 0 → Fg – F = 0
Fg = F
Aunque la fuerza centrífuga se considere una pseudofuerza, sus efectos son bastante reales, como se puede apreciar en los siguientes ejemplos:
– En cualquier juego giratorio de un parque de diversiones, la fuerza centrífuga está presente. Ella se encarga de que “huyamos del centro” y ofrece una resistencia constante si se intenta caminar hacia el centro de un carrusel en movimiento. En el siguiente péndulo se puede apreciar la fuerza centrífuga:

– El efecto Coriolis surge de la rotación terrestre, que hace que la Tierra deje de ser un marco inercial. Entonces aparece la fuerza de Coriolis, que una pseudo-fuerza que desvía lateralmente los objetos, al igual que sucede con las personas que tratan de caminar sobre una plataforma giratoria.

Un automóvil que gira con aceleración A hacia la derecha lleva un juguete de peluche colgando del espejo retrovisor interno. Dibuje y compare los diagramas de cuerpo libre del juguete visto desde:
a) El marco de referencia inercial de un observador parado en la vía.
b) Un pasajero que viaja en el automóvil.
Solución a
Un observador de pie en la vía advierte que el juguete se mueve aceleradamente, con aceleración A hacia la derecha.
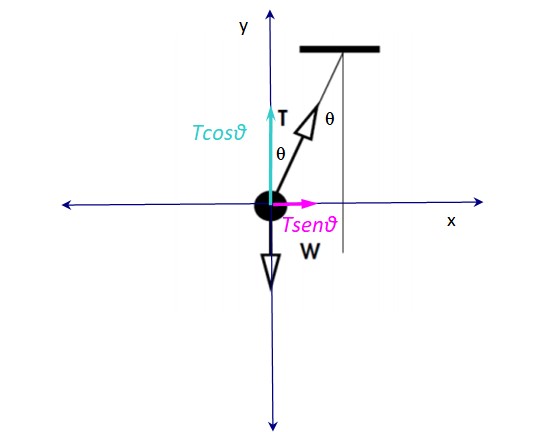
Hay dos fuerzas actuando sobre el juguete: por un lado la tensión en la cuerda T y el peso vertical hacia abajo W. El peso está equilibrado con la componente vertical de la tensión Tcosθ, por lo tanto:
W – Tcosθ= 0
La componente horizontal de la tensión: T. senθ es la fuerza no equilibrada responsable de la aceleración hacia la derecha, por lo tanto la fuerza centrípeta es:
Fc= T.senθ = mac
Solución b
Para un pasajero en el carro, el juguete cuelga en equilibrio y el diagrama es como sigue:
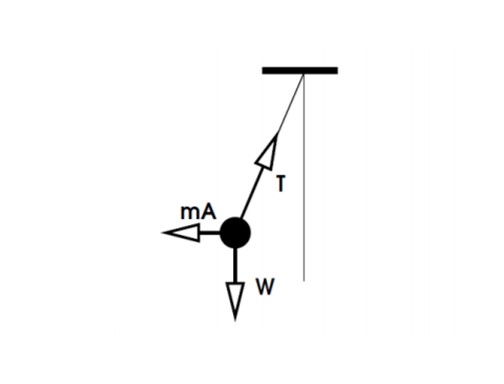
Tal como en el caso anterior, el peso y la componente vertical de la tensión se compensan. Pero la componente horizontal se equilibra con la fuerza ficticia Fg = mA, de tal forma que:
-mA + Tsenθ = 0
Fg = mA
Una moneda está en el borde de un antiguo tocadiscos de vinilos, cuyo radio es de 15 cm y está rotando a razón de 33 revoluciones / minuto. Encuentre el coeficiente de roce estático mínimo necesario para que la moneda se mantenga en su sitio, utilizando el marco de referencia solidario a la moneda.
Solución
En la figura está el diagrama de cuerpo libre para un observador que se mueve con la moneda. La normal N que el tocadiscos ejerce verticalmente hacia arriba se equilibra con el peso W, mientras que la fuerza centrífuga Fg es compensada por el roce estáticoFroce.
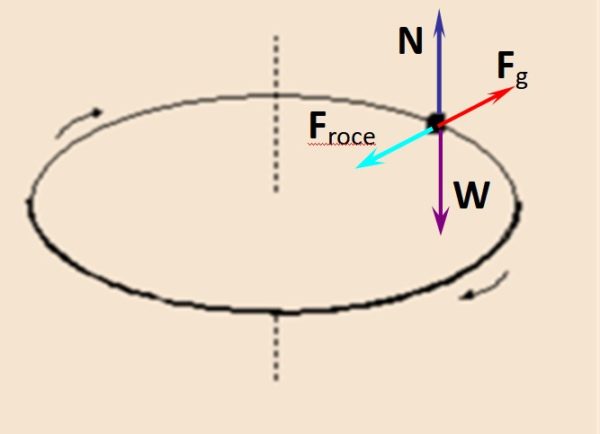
N – W = 0
Froce – Fg = 0
La magnitud de la fuerza centrífuga es mv2/R, como se dijo al comienzo, entonces:
Froce = Fg = mv2/R
Por otra parte, la fuerza de roce estático viene dada por:
Froce = μs.N
Donde μs es el coeficiente de roce estático, una cantidad sin dimensiones cuyo valor depende de cómo son las superficies en contacto. Sustituyendo esta ecuación queda:
μs.N= mv2/R → μs = mv2/R.N
Faltaría por determinar la magnitud de la normal, que está relacionada con el peso según N = mg. Sustituyendo nuevamente:
μs = mv2/R.mg → μs = v2/Rg
De vuelta al enunciado, este informa que la moneda gira a razón de 33 revoluciones /minuto, que es la velocidad angular o frecuencia angular ω, relacionada con la rapidez lineal v:
v=ω.R=33 rev/min . 2π radianes/rev . 15 cm . (1 min/60 s) = 51. 8 cm/s
μs = v2/Rg=(51.8 cm/s)2/ (15cm x 981 cm/s2)= 0.18
Los resultados de este ejercicio habrían sido los mismos de haber seleccionado un sistema de referencia inercial. En tal caso la única fuerza capaz de originar aceleración hacia el centro es el roce estático.
Tal como hemos venido diciendo, la fuerza centrífuga es una fuerza ficticia, que no aparece en los marcos inerciales, que son los únicos en los cuales las leyes de Newton son válidas. En ellos, la fuerza centrípeta se encarga de proporcionar al cuerpo la aceleración necesaria hacia el centro.
La fuerza centrípeta no es una fuerza distinta a las ya conocidas. Al contrario, son precisamente estas las que hacen el papel de fuerzas centrípetas cuando corresponde. Por ejemplo, la gravedad que hace orbitar a la Luna en torno a la Tierra, la tensión en una cuerda mediante la que se gira una piedra, el roce estático y la fuerza electrostática.
Sin embargo, como en la práctica abundan los sistemas de referencia acelerados, las fuerzas ficticias tienen efectos muy reales. Para muestra, he aquí tres aplicaciones importantes en las que tienen efectos tangibles:
Las centrifugadoras son instrumentos ampliamente utilizados en el laboratorio. La idea es hacer que una mezcla de sustancias gire a gran velocidad y aquellas sustancias con mayor masa, experimentan una mayor fuerza centrífuga, de acuerdo a la ecuación descrita al comienzo.
Entonces las partículas más masivas tenderán a alejarse del eje de rotación, quedando así separadas de las más livianas, las cuales permanecerán más cerca del centro.
Las lavadoras automáticas poseen diversos ciclos de exprimir. En ellos la ropa es centrifugada para eliminar el agua remanente. A más revoluciones del ciclo, menos húmeda quedará la ropa al finalizar el lavado.

Los autos toman mejor las curvas en las carreteras, gracias a que la vía se inclina un poco hacia el centro de la curva, lo que se conoce como peralte. De esta manera el auto no depende exclusivamente del rozamiento estático entre los neumáticos y la vía para completar el giro sin salirse de la curva.
- Acosta, Victor. Construcción de una guía didáctica sobre fuerza centrífuga para estudiantes de ciclo V grado 10.Recuperado de: bdigital.unal.edu.co.
- Toppr. Laws of Motion: Circular Motion. Recuperado de: toppr.com.
- Resnick, R. (1999). Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Universidad Autónoma del Estado de Hidalgo. Fuerza centrífuga. Recuperado de: uaeh.edu.mx
- Wikipedia. Centrifugadoras. Recuperado de: es.wikipedia.org.
