Coordenadas cilíndricas: sistema, cambio y ejercicios

Las coordenadas cilíndricas sirven para ubicar puntos en el espacio tridimensional y constan de una coordenada radial ρ, una coordenada azimutal φ y una coordenada de altura z.

Un punto P ubicado en el espacio se proyecta ortogonalmente sobre el plano XY dando lugar al punto P’ en ese plano. La distancia desde el origen hasta el punto P’ define la coordenada ρ, mientras que el ángulo que forma el eje X con la semirrecta OP’ define la coordenada φ. Por último, la coordenada z es la proyección ortogonal del punto P sobre el eje Z. (ver figura 1).

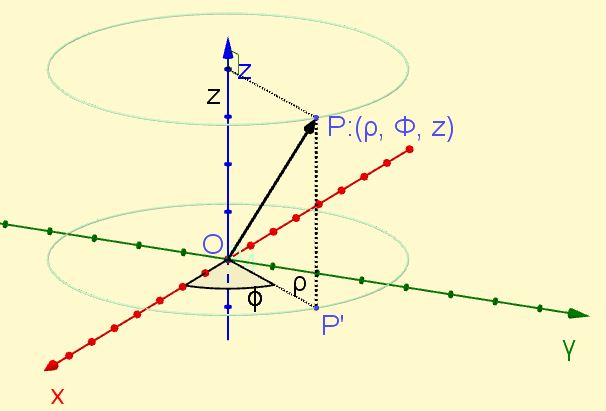
La coordenada radial ρ siempre es positiva, la coordenada azimutal φ varía desde cero radianes hasta dos pi radianes, mientras la coordenada z puede tomar cualquier valor real:

0 ≤ ρ ∞

0 ≤ φ 2π

– ∞ z + ∞

Índice del artículo

• 1 Cambio de coordenadas
  • 1.1 Base vectorial en coordenadas cilíndricas
• 2 Ejemplos
  • 2.1 Ejemplo 1
  • 2.2 Ejemplo 2
• 3 Ejercicios resueltos
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2
  • 3.3 Ejercicio 3
  • 3.4 Ejercicio 4
• 4 Referencias

Cambio de coordenadas

Es relativamente sencillo obtener las coordenadas cartesianas (x, y, z) de un punto P a partir de sus coordenadas cilíndricas (ρ, φ, z):

x = ρ cos(φ)

y = ρ sen(φ)

z = z

Pero también es posible obtener las coordenadas polares (ρ, φ, z) partiendo del conocimiento de las coordenadas cartesianas (x, y, z) de un punto P:

ρ = √(x² + y²)

φ = arctan( y/x )

z = z

Base vectorial en coordenadas cilíndricas

Se define la base de vectores unitarios cilíndricos Uρ, Uφ, Uz.

El vector Uρ es tangente a la línea φ = ctte y z = ctte (apuntando radialmente hacia afuera), el vector Uφ es tangente a la línea ρ = ctte y z = ctte y por último Uz tiene la misma dirección del eje Z.

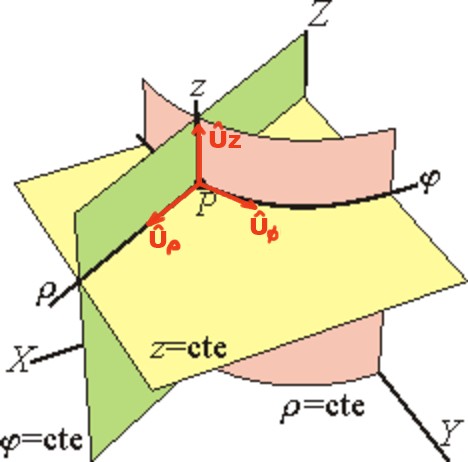
En la base unitaria cilíndrica, el vector de posición r de un punto P se escribe vectorialmente así:

r = ρ Uρ + 0 Uφ + z Uz

Por otra parte, un desplazamiento infinitesimal dr a partir del punto P se expresa de la siguiente manera:

dr = dρ Uρ + ρ dφ  Uφ + dz Uz

De forma similar, un elemento infinitesimal de volumen dV en coordenadas cilíndricas es:

dV = ρ dρ dφ dz

Ejemplos

Hay infinidad de ejemplos del uso y aplicación de las coordenadas cilíndricas. En cartografía, por ejemplo, se usa la proyección cilíndrica, basada justamente en estas coordenadas. Existen más ejemplos:

Ejemplo 1

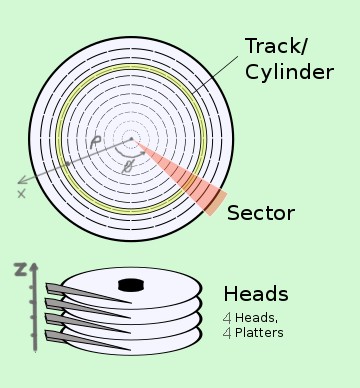
Las coordenadas cilíndricas tienen aplicaciones en la tecnología. Como ejemplo se tiene el sistema CHS (Cylinder-Head-Sector) de ubicación de datos en un disco duro, el cual en realidad consiste en varios discos:

– El cilindro o pista corresponde a la coordenada ρ.

– El sector corresponde a la posición φ del disco que gira a elevada velocidad angular.

– La cabeza corresponde a la posición z del cabezal de lectura en el disco correspondiente.

Cada byte de información tiene una dirección precisa en coordenadas cilíndricas (C, S, H).

Ejemplo 2

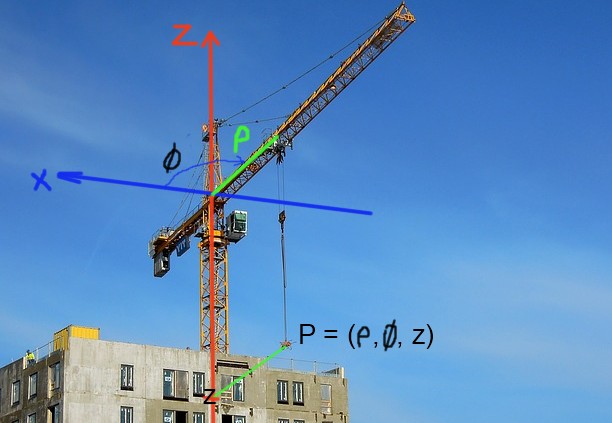
Las grúas de construcción fijan la posición de la carga en coordenadas cilíndricas. La posición horizontal queda definida por la distancia al eje o flecha de la grúa ρ y por su posición angular φ respecto de algún eje de referencia. La posición vertical de la carga queda determinada por la coordenada z de la altura.

Ejercicios resueltos

Ejercicio 1

Se tienen los puntos P1 de coordenadas cilíndricas ( 3, 120º, -4) y el punto P2 de coordenadas cilíndricas ( 2, 90º, 5). Hallar la distancia euclidiana entre estos dos puntos.

Solución: En primer lugar, se procede a encontrar las coordenadas cartesianas de cada punto siguiendo la fórmula que se dio más arriba.

P1 = ( 3* cos 120º,  3* sen 120º, -4 ) = ( -1.5, 2.60, -4 )

P2 = ( 2* cos 90º,  2* sen 90º, 5 ) = ( 0, 2, 5 )

La distancia euclidiana entre P1 y P2 es:

d(P1, P2) = √( (0 – (-1.5))²+(2 – 2.60)²+(5 -(-4))² ) =…

… √(2.25+0.36+81) = 9.14

Ejercicio 2

El punto P tiene coordenadas cartesianas ( -3, 4, 2 ). Hallar las coordenadas cilíndricas correspondientes.

Solución: Se procede a encontrar las coordenadas cilíndricas usando las relaciones dadas más arriba:

ρ = √(x² + y²) = √((-3)² + 4²) = √(9 + 16) = √(25) = 5

φ = arctan( y/x ) = arctan( 4/(-3)) = -53.13º + 180º = 126.87º

z = 2

Cabe recordar que la función arcotangente es multivaluada de periodicidad 180º. Además, el ángulo φ debe pertenecer al segundo cuadrante, ya que las coordenadas x e y del punto P están en ese cuadrante. Esta es la razón por la que se ha sumado 180º al resultado φ.

Ejercicio 3

Expresar en coordenadas cilíndricas y en coordenadas cartesianas la superficie de un cilindro de radio 2 y cuyo eje coincide con el eje Z.

Solución: Se entiende que el cilindro tiene una extensión infinita en la dirección z, por lo que la ecuación de dicha superficie en coordenadas cilíndricas es:

ρ = 2

Para obtener la ecuación cartesiana de la superficie cilíndrica se toma el cuadrado de ambos miembros de la ecuación anterior:

ρ² = 4

Multiplicamos por 1 ambos miembros de la igualdad anterior y aplicamos la identidad trigonométrica fundamental (sen²(φ) + cos²(φ) =1 ):

1 * ρ² = 1 * 4

( sen²(φ) + cos²(φ) ) * ρ² = 1 * 4

Se desarrolla el paréntesis para obtener:

( ρ sen(φ) )² + ( ρ cos(φ) )² = 4

Recordamos que el primer paréntesis ( ρ sen(φ) ) es la coordenada y de un punto en coordenadas polares, mientras que el paréntesis ( ρ cos(φ) ) representa la coordenada x, de modo que nos queda la ecuación del cilindro en coordenadas cartesianas:

y² + x² = 2²

No debe confundirse la ecuación anterior con la de una circunferencia en el plano XY, ya que en este caso quedaría así: { y² + x² = 2² ;  z=0 }.

Ejercicio 4

Un cilindro de radio R = 1 m y altura H = 1m tiene su masa distribuida radialmente de acuerdo a la siguiente ecuación D(ρ) = C (1 – ρ/R) donde C es una constante de valor C = 1 kg/m³. Hallar la masa total del cilindro en kilogramos.

Solución: Lo primero es darse cuenta que la función D(ρ) representa la densidad volumétrica de masa, y que la masa densidad está distribuida en cascarones cilíndricos de densidad decreciente del centro a la periferia. Un elemento infinitesimal de volumen de acuerdo a la simetría del problema es:

dV =  ρ dρ 2π H

De allí se tiene que, la masa infinitesimal de un cascarón cilíndrico será:

dM = D(ρ) dV

Por lo que la masa total del cilindro, quedará expresada mediante la siguiente integral definida:

M = ∫_o^R D(ρ) dV = ∫_o^R C (1 – ρ/R) ρ dρ 2π H = 2π H C ∫_o^R (1 – ρ/R) ρ dρ

La solución de la integral indicada no es difícil de obtener, siendo su resultado:

∫_o^R (1 – ρ/R) ρ dρ = (⅙)R²

Incorporando este resultado en la expresión de la masa del cilindro se obtiene:

M = 2π H C (⅙)R² = ⅓ π H C R² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Referencias

1. Arfken G and Weber H. (2012). Mathematical methods for physicists. A comprehensive guide. 7th edition. Academic Press. ISBN 978-0-12-384654-9
2. Cálculo cc. Problemas resueltos de coordenadas cilíndricas y esféricas. Recuperado de: calculo.cc
3. Weisstein, Eric W. “Cylindrical Coordinates.” From MathWorld–A Wolfram Web. Recuperado de: mathworld.wolfram.com
4. wikipedia. Cylindrical coordinate system. Recuperado de: en.wikipedia.com
5. wikipedia. Vector fields in cylindrical and spherical coordinates. Recuperado de: en.wikipedia.com