Momento de inercia: fórmulas, ecuaciones y ejemplos de cálculo

El momento de inercia de un cuerpo rígido respecto a cierto eje de rotación, representa su resistencia a cambiar su velocidad angular alrededor de dicho eje. Es proporcional a la masa y también a la ubicación del eje de giro, ya que el cuerpo, según su geometría, puede rotar más fácilmente en torno a ciertos ejes que en otros.

Supongamos un objeto extenso (que consta de muchas partículas) el cual puede rotar alrededor de un eje. Supongamos que actúa una fuerza F, aplicada tangencialmente sobre el elemento de masa Δm_i, que produce un torque o momento, dado por τ_neto = ∑r_i x F_i. El vector r_i es la posición de Δm_i (ver figura 2).

Dicho momento es perpendicular al plano de rotación (dirección +k = saliendo del papel). Ya que la fuerza y el vector posición radial siempre son perpendiculares, el producto cruz queda:

τ_neto = ∑ F_i r_ik =  ∑ (Δm_i a_i) r_i  k = ∑ Δm_i (a_i r_i ) k

La aceleración a_i representa la componente tangencial de la aceleración, ya que la aceleración radial no contribuye al torque. En función de la aceleración angular α, podemos indicar que:

a_i = α r_i

Por lo tanto el torque neto queda así:

 τ_neto = ∑ Δm_i (α r_i²) k = (∑ r_i² Δm_i)α k

La aceleración angular α es la misma para todo el objeto, por lo tanto no está afectada por el subíndice “i” y puede salir de la sumatoria, la cual es precisamente el momento de inercia del objeto simbolizada con la letra I:

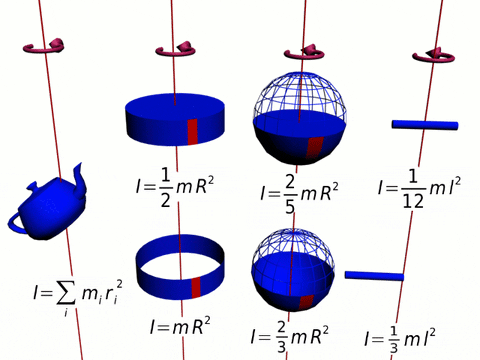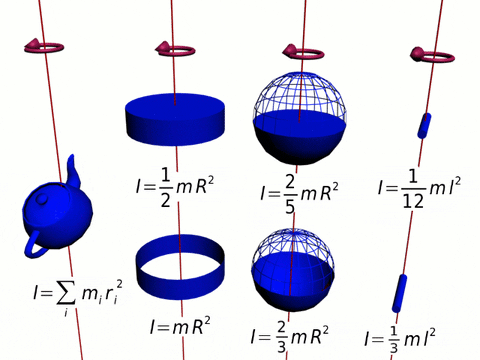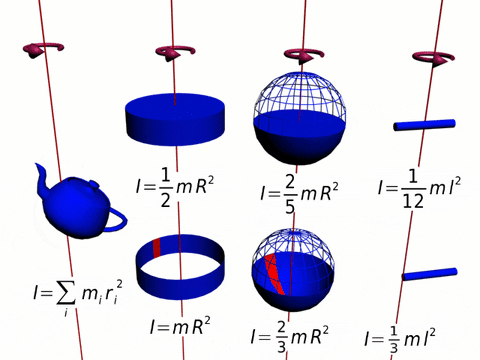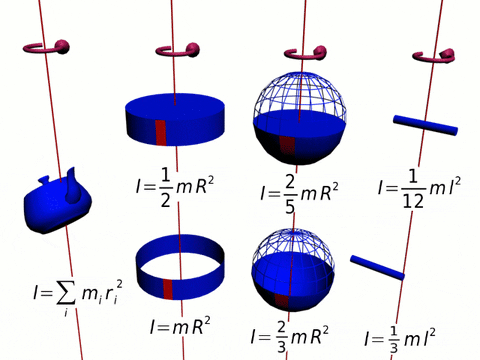
I = ∑ r_i² Δm_i

Este es el momento de inercia de una distribución de masa discreta. Cuando la distribución es continua, la sumatoria se reemplaza con una integral y Δm se convierte en un diferencial de masa dm. La integral se efectúa sobre todo el objeto:

I = ∫_M(r²)dm

Las unidades del momento de inercia en el Sistema Internacional SI son kg x m². Se trata de una cantidad escalar y positiva, ya que es el producto de una masa por el cuadrado de una distancia.

Índice del artículo

• 1 Ejemplos de cálculo
  • 1.1 Momento de inercia de una barra delgada respecto a un eje que pasa por su centro
  • 1.2 Momento de inercia de un disco respecto a un eje que pasa por su centro
  • 1.3 Momento de inercia de una esfera sólida respecto a un diámetro
  • 1.4 Momento de inercia de un cilindro sólido respecto al eje axial
  • 1.5 Momento de inercia de una lámina rectangular respecto a un eje que pasa por su centro
  • 1.6 Momento de inercia de una lámina cuadrada respecto a un eje que pasa por su centro
• 2 Teoremas del momento de inercia
  • 2.1 Teorema de Steiner
  • 2.2 Teorema de los ejes perpendiculares
• 3 Ejercicio resuelto
• 4 Referencias

Ejemplos de cálculo

Un objeto extendido, como una barra, disco, esfera u otro, cuya densidadρ es constante y sabiendo que la densidad es el cociente masa – volumen, el diferencial de masa dm se escribe como:

ρ = dm/dV → dm = ρdV

Sustituyendo en la integral para el momento de inercia, tenemos:

 I = ∫r² ρdV = ρ ∫r²dV

Esta es una expresión general, válida para un objeto tridimensional, cuyos volumen V y posición r son funciones de las coordenadas espaciales x, y y z. Nótese que al ser constante, la densidad queda fuera de la integral.

La densidad ρ se conoce también como densidad volumétrica, pero si el objeto es muy plano, como una lámina o muy delgado y estrecho como una varilla, se pueden utilizar otras formas de densidad, veamos:

– Para una lámina muy fina, la densidad a utilizar es σ, la densidad superficial (masa por unidad de área) y dA es el diferencial de área.

– Y si se trata de una barra delgada, donde solamente la longitud es relevante, se utiliza la densidad lineal de masa λ y un diferencial de longitud, según el eje utilizado como referencia.

En los ejemplos que siguen se considera que todos los objetos son rígidos (no deformables) y tienen densidad uniforme.

Momento de inercia de una barra delgada respecto a un eje que pasa por su centro

Aquí vamos a calcular el momento de inercia de una barra delgada, rígida, homogénea, de longitud L y masa M, respecto a un eje que pasa por el medio.

En primer lugar es preciso establecer un sistema de coordenadas y construir una figura con la geometría adecuada, como esta:

Se escogió el eje x a lo largo de la barra y el eje y como eje de rotación. El procedimiento para establecer la integral requiere también elegir un diferencial de masa sobre la barra, llamado dm, el cual tiene una longitud diferencial dx y se localiza en la posición x arbitraria, respecto al centro x=0.

De acuerdo a la definición de densidad de masa lineal λ:

λ = M/L

Al ser uniforme la densidad, lo que es válido para M y L, también lo es para dm y dx:

λ = dm/dx → dm = λdx.

Por otro lado, el elemento de masa está en la posición x, entonces al sustituir esta geometría en la definición, tenemos una integral definida, cuyos límites son los extremos de la barra según el sistema coordenado:

Sustituyendo la densidad lineal  λ=M/L:

Para hallar el momento de inercia de la barra respecto a otro eje de rotación, por ejemplo uno que pase por uno de sus extremos, se puede utilizar el teorema de Steiner (ver ejercicio resuelto al final) o bien efectuar un cálculo directo semejante al mostrado aquí, pero modificando adecuadamente la geometría.

Momento de inercia de un disco respecto a un eje que pasa por su centro

Un disco muy delgado, de espesor despreciable es una figura plana. Si la masa está distribuida uniformemente por toda la superficie de área A, la densidad de masa σ es:

σ = M/A

Tanto dm como dA corresponden a la masa y al área del anillo diferencial mostrado en la figura. Supondremos que todo el conjunto gira alrededor del eje y.

Se puede imaginar que el disco está compuesto que muchos anillos concéntricos de radio r, cada uno con su respectivo momento de inercia. Sumando las contribuciones de todos los anillos hasta llegar al de radio R, se tendrá el momento de inercia total del disco.

 σ=dm/dA→ dm = σdA

Donde M representa la totalidad de la masa del disco. El área de un disco depende de su radio r como:

A = π.r²

Derivando respecto a r:

dA /dr = 2= 2π.r → dA =  2π.rdr

Sustituyendo lo anterior en la definición de I:

Sustituyendo σ =  M/(π.R² ) queda:

Momento de inercia de una esfera sólida respecto a un diámetro

Una esfera de radio R puede considerarse como una serie de discos apilados uno encima de otro, donde cada disco de masa infinitesimal dm, radio r y espesor dz, tiene un momento de inercia dado por:

 dI_disco = (½) r²dm

Para encontrar este diferencial, simplemente se tomó la fórmula de la sección anterior y se sustituyeron M y R por dm y r, respectivamente. Un disco como este se aprecia en la geometría de la figura 5.

Al sumar todos los momentos de inercia infinitesimales de discos apilados, se obtiene el momento de inercia total de la esfera:

I_esfera = ∫dI_disco

Lo cual equivale a:

I = ∫_esfera (½) r²dm

Para resolver la integral se necesita expresar dm apropiadamente. Como siempre, se logra a partir de la densidad:

ρ = M/V = dm/dV → dm = ρ.dV

El volumen de un disco diferencial es:

dV = Área de la base x altura

La altura del disco es el espesor dz, mientras que el área de la base es πr², por lo tanto:

 dV = πr²dz

Y sustituyendo en la integral planteada quedaría así:

 I = ∫_esfera(½) r²dm = ∫(½) r²(ρπr²dz)

Pero antes de integrar, hay que observar que r –el radio del disco- depende de z y R –el radio de la esfera-, como se ve de la figura 5. Mediante el teorema de Pitágoras:

R² = r² + z² → r² = R² – z²

 Que nos lleva a:

 I = ∫_esfera(½)ρ r²(πr²dz)= ∫_esfera(½)ρ π r⁴dz= ∫_esfera(½)ρ π (R² – z²)² dz

Para integrar sobre toda la esfera, notamos que z varía entre –R y R, por lo tanto:

Sabiendo que ρ = M/V = M /[(4/3)πR³] finalmente se obtiene, luego de simplificar:

Momento de inercia de un cilindro sólido respecto al eje axial

Para este objeto se utiliza un método parecido al que se usó para la esfera, solo que esta vez es más sencillo si el cilindro se imagina formado por cascarones cilíndricos de radio r, espesor dr y altura H, como si fueran las capas de una cebolla.

El volumen dV de una capa cilíndrica es:

dV = 2π.rL.dr

Por lo tanto la masa del cascarón es:

 dm = ρ.dV= ρ. 2π.r.L.dr

Se sustituye esta expresión en la definición de momento de inercia:

La ecuación anterior señala que el momento de inercia del cilindro no depende de su longitud, sino de su masa y de su radio solamente. Si L cambiase, el momento de inercia respecto al eje axial seguiría siendo el mismo. Por esta razón, I del cilindro coincide con el del disco delgado previamente calculado.

Momento de inercia de una lámina rectangular respecto a un eje que pasa por su centro

Se ha escogido al eje y horizontal como eje de rotación. La figura a continuación muestra la geometría necesaria para llevar a cabo la integración:

El elemento de área señalado en rojo es rectangular. Su área es base x altura, por lo tanto:

 dA = a.dz

Por lo tanto el diferencial de masa es:

dm = σ.dA = σ.(a.dz)

En cuanto a la distancia del elemento de área al eje de rotación, siempre es z. Sustituimos todo esto en la integral del momento de inercia:

Ahora se sustituye la densidad de masa superficial σ por:

σ = M/ab

Y definitivamente queda así:

Nótese que es como el de la barra delgada.

Momento de inercia de una lámina cuadrada respecto a un eje que pasa por su centro

Para un cuadrado de lado L, en la expresión anterior válida para un rectángulo, simplemente se sustituye el valor de b por el de L:

Teoremas del momento de inercia

Hay dos teoremas especialmente útiles para simplificar el cálculo de momentos de inercia respecto a otros ejes, que de otra manera podrían resultar complicados de hallar por la falta de simetría. Estos teoremas son:

Teorema de Steiner

Llamado también teorema de los ejes paralelos, relaciona el momento de inercia de respecto a un eje con otro que pase por el centro de masa del objeto, siempre y cuando los ejes sean paralelos. Para aplicarlo se necesita conocer la distancia D entre ambos ejes y desde luego la masa M del objeto.

Sea I_z el momento de inercia de un objeto extendido respecto al eje z, I_CM el momento de inercia respecto a un eje que pasa por el centro de masas (CM) de dicho objeto, entonces se cumple que:

I_z = I_CM + MD²

O en la notación de la siguiente figura: I_z’ = I_z + Md²

Teorema de los ejes perpendiculares

Este teorema se aplica a superficies planas y dice así: el momento de inercia de un objeto plano alrededor de un eje perpendicular a él, es la suma de los momentos de inercia alrededor de dos ejes perpendiculares al primer eje:

I_z = I_x + I_y

Si el objeto posee simetría tal que I_x e I_y son iguales, entonces se cumple que:

I_z = 2I_x

Ejercicio resuelto

Hallar el momento de inercia de la barra respecto a un eje que pasa por uno de sus extremos, como la mostrada en la figura 1 (abajo y a la derecha) y la figura 10.

Solución:

Ya tenemos el momento de inercia de la barra alrededor de un eje que pasa por su centro geométrico. Puesto que la barra es homogénea, su centro de masa se encuentra en dicho punto, entonces este será nuestro I_CM para aplicar el teorema de Steiner.

Si la longitud de la barra es L, el eje z está a una distancia D = L/2, por lo tanto:

I_z = I_CM + MD²= (1/12)ML²+M(L/2)²=(1/3)ML²

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 313-340
2. Rex, A. 2011. Fundamentos de Física. Pearson. 190-200.
3. Parallel Axis Theorem. Recuperado de: hyperphysics.phy-astr.gsu.edu.
4. Serway, R. 2018. Física para Ciencias e Ingeniería. Volumen 1. Cengage.
5. Universidad de Sevilla. Momento de inercia de sólidos esféricos. Recuperado de: laplace.us.es.
6. Universidad de Sevilla. Momento de inercia de un sistema de partículas. Recuperado de: laplace.us.es.
7. Wikipedia. Parallel axis theorem. Recuperado de: en.wikipedia.org