Geometría euclidiana: concepto, historia, elementos, ejemplos

¿Qué es la geometría euclidiana?
La geometría euclidiana es la que se rige por los postulados por Euclides de Alejandría, geómetra griego que vivió hacia el 300 a.C, en cuyo honor se nombra esta disciplina, pues fue el primero en sistematizarla.
Esta rama de las matemáticas estudia las propiedades de las rectas, planos, ángulos y figuras geométricas como polígonos, circunferencias y demás cónicas. De allí su importancia en la ciencia y de la ingeniería, cuyo desarrollo impulsó notablemente.
Por otro lado, la geometría euclidiana fue la primera ciencia exacta, ya que con ella se inició el camino de la sistematización de la ciencia, así como el uso de la lógica para demostrar, a partir de unos pocos axiomas, numerosas proposiciones llamadas teoremas, a fin de describir las propiedades de los objetos geométricos.
Historia
La geometría tiene una larga historia, pues el interés de la humanidad en ella es muy antiguo y el eje central de la geometría euclidiana es la obra Elementos, del sabio Euclides de Alejandría, ciudad situada en Egipto, y quien vivió en el siglo IV a.C.
Para la época se conocían las propiedades más importantes de numerosas figuras y cuerpos geométricos. Existía un extenso conocimiento acerca de la geometría, pero todo era de carácter empírico y carecía de sistematización.
Entonces, el rey de Egipto Ptolomeo I encomendó al ya célebre maestro Euclides, cuya escuela estaba en Alejandría, que organizara todo el saber matemático y geométrico disponible hasta el momento, incluyendo teoremas y propiedades.
Euclides puso manos a la obra y junto a sus discípulos, escribió su obra Elementos, a la que dividió en trece libros, a modo de capítulos. Esta obra se convertiría en un referente de la geometría para las futuras generaciones.
Los Elementos de Euclides
El contenido de los Elementos se organiza de la siguiente forma:
- En los libros I al IV se desarrolla la geometría plana.
- En los libros V y VI la teoría de la proporción.
- Los libros VII al IX están dedicados a la aritmética.
- La inconmesurabildad aparece en el libro X,
- La geometría del espacio en los libros XI al XIII.
La geometría euclidiana fue la base para muchos desarrollos geométricos posteriores y en la actualidad se sigue enseñando en todas las escuelas del mundo.
Además tiene la virtud de ser la primera obra en incluir cuidadosas demostraciones a base de razonamientos lógicos, y también en dar coherencia al cuerpo de conocimientos geométricos y matemáticos de aquel entonces.
Elementos básicos de la geometría euclidiana
La geometría euclidiana se construye alrededor de cuatro elementos básicos, descritos en el libro I de los Elementos:
- Punto
- Recta
- Plano
- Espacio
1. Punto
Un punto carece de dimensiones o partes y se distingue de otro punto simplemente por su ubicación. Si dos puntos A y B son diferentes, es porque tienen posiciones diferentes, las cuales se indican a través de las conocidas coordenadas cartesianas (x, y) si el punto está en el plano, o las coordenadas (x,y,z) si está en el espacio.
Es de resaltar que el sistema cartesiano no es parte de los Elementos de Euclides, sino que apareció mucho después allá por los años 1600 y se le debe a René Descartes.
2. Recta
La recta es una colección infinita de puntos, y únicamente tiene longitud, no anchura. Suele dibujarse una parte de ella, con flechas en ambos señalando que la recta prosigue indefinidamente.
3. Plano
Un plano es una superficie ilimitada, por lo que posee dos dimensiones y del cual se representa una porción, mediante un cuadrado o un rectángulo.
Allí, en el plano, se encuentran multitud de figuras geométricas, como rectas, curvas abiertas y cerradas y polígonos, entre otros.
4. Espacio
Por último, está el espacio con sus tres dimensiones, capaz de albergar a todos los puntos. Contiene a los planos y a los cuerpos geométricos caracterizados por su volumen, como los poliedros, las esferas y más.
Estas se pueden considerar las definiciones básicas de la geometría euclidiana, pero además de estas, Euclides ofrece unas 150 definiciones variadas en su obra.
Nociones comunes
Consisten en hechos obvios e intuitivos, que no pertenecen propiamente al ámbito de la geometría y que son usados a medida que desarrollan los conceptos. Se refieren a “cosas” en un contexto muy amplio:
- Cosas iguales a otra cosa, son iguales entre sí.
- Si se añaden cosas a otro conjunto de cosas, y todas ellas son iguales, lo que resulta también son iguales.
- Si se sustraen cosas iguales entre sí, lo que resta también es igual.
- Cuando las cosas coinciden entre sí, es porque son iguales.
- El todo siempre es mayor que las partes, tomadas por separado.
Postulados de la geometría euclidiana
Los postulados o axiomas son afirmaciones simples que se consideran verdaderas y evidentes, por lo que no requieren demostración.
Ellos constituyen la base de la geometría euclidiana y Euclides establece cinco en su libro I:
- Sean dos puntos distintos A y B, existe solo una recta que pasa por ellos, es decir, dos puntos determinan una recta.
- Cualquier segmento rectilíneo puede prolongarse de forma indefinida para constituir una recta, por lo tanto, todo segmento pertenece a alguna recta.
- Si se tienen dos puntos diferentes O y A, siempre se puede dibujar una circunferencia con centro en O y radio igual al segmento OA.
- Todos los ángulos rectos son congruentes entre sí.
- Dada una recta L y un punto P que no pertenece a ella, siempre es posible hallar una recta M que pasa por P y que sea paralela a L.
El último postulado, sobre todo en su versión original, no luce tan simple como los demás. En él se afirma que:
“Si una línea recta que cae sobre otras dos rectas, hace que los dos ángulos interiores del mismo lado sean menores que dos ángulos rectos, dichas líneas rectas, extendidas indefinidamente, se encuentran (intersectan) en el lado en el que están los ángulos menores que los dos ángulos rectos”.
Es decir, originalmente el postulado 5 establece la condición para que dos rectas no sean paralelas. Pero resulta más claro cuando se escribe de tal forma que ilustra lo contrario, es decir, el paralelismo de las rectas.
Ejemplos de geometría euclidiana
Ejemplo 1
Se tienen tres puntos distintos, etiquetados con las letras A, B y C.
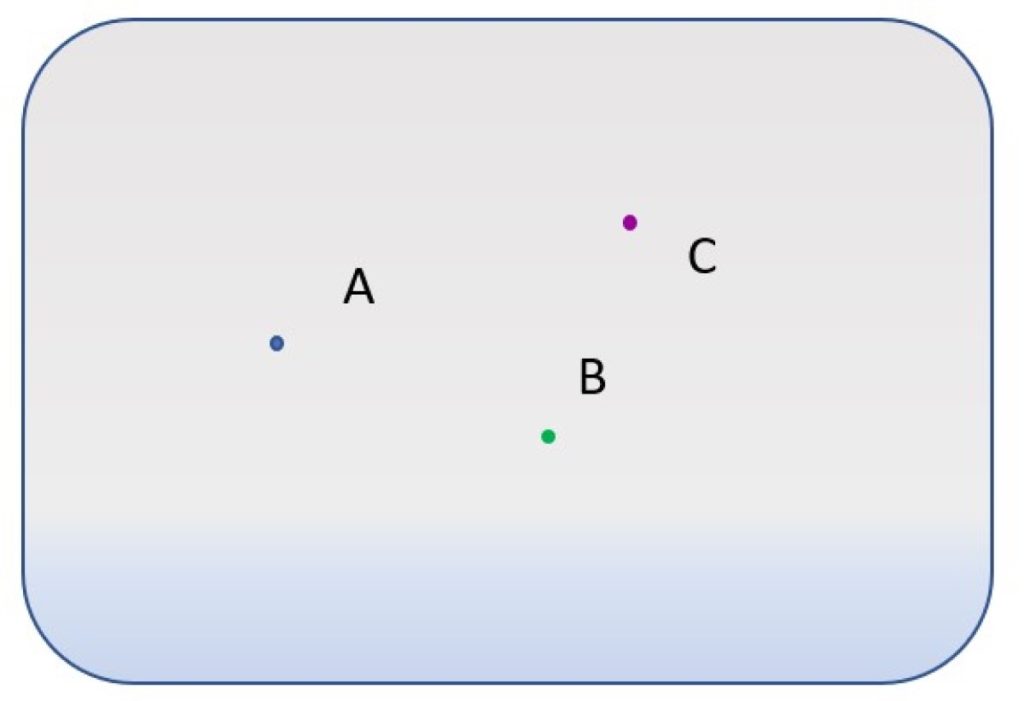
- ¿Cuántas rectas diferentes pasan por el punto A?
- ¿Y cuántas se pueden trazar entre los puntos A y B? ¿Y entre A y C?
- ¿Es posible trazar una recta a la que pertenezcan simultáneamente los puntos A, B y C?
Respuesta a
De acuerdo al postulado I, se pueden trazar infinitas rectas que pasen por A, ya que se requieren dos puntos para determinar una recta.
Respuesta b
Entre A y B solamente se puede trazar una recta. Y entre A y C también.
Respuesta c
No es posible que una recta contenga a A, B y C al mismo tiempo.
Ejemplo 2
Se pide construir paso a paso un triángulo equilátero (todos sus lados son iguales), conociendo uno de sus lados, que es el segmento AB e indicando en cada paso el postulado o noción común empleado en la construcción.
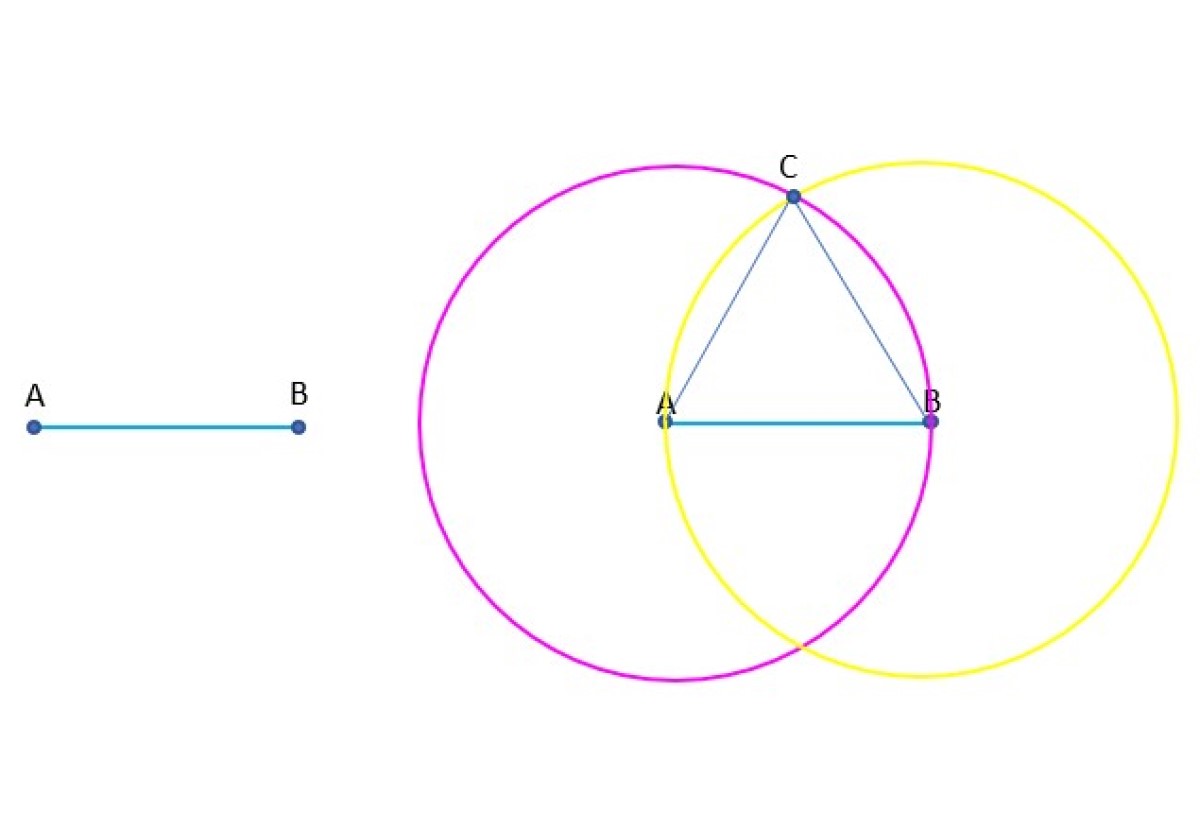
Respuesta
Paso 1
Se traza una circunferencia con centro en A y radio AB. Esto siempre es posible, según el postulado III.
Paso 2
Se traza otra circunferencia con centro en B y radio AB, y nuevamente se aplica el postulado III.
Paso 3
Ambas circunferencias, que tienen el mismo radio, se cortan en el punto C. Ahora se pueden trazar segmentos que unen C con A y B respectivamente, según el postulado I.
Estos segmentos son radios de la circunferencia y por lo tanto las medidas de AC y BC son iguales a la de AB, de acuerdo a la noción común 1. Luego el triángulo ABC es equilátero.
