Fricción viscosa (fuerza): coeficiente y ejemplos
La fricción viscosa surge cuando un objeto sólido se mueve en medio de un fluido -un gas o un líquido-. Puede modelarse como una fuerza proporcional al negativo de la velocidad del objeto o al cuadrado de la misma.
El uso de uno u otro modelo depende de ciertas condiciones, como el tipo de fluido en que se mueva el objeto y si es o no muy rápido. El primer modelo se conoce como resistencia lineal, y en él la magnitud del roce viscoso Froce viene dada por:
Froce = γv

Aquí γ es la constante de proporcionalidad o coeficiente de fricción viscosa y v es la rapidez del objeto. Es aplicable a cuerpos que se mueven a bajas velocidades en fluidos con régimen laminar.
En el segundo modelo, conocido como resistencia cuadrática o ley de Rayleigh, la magnitud de la fuerza de roce se calcula según:
Froce = ½ ρ.A.Cd.v2
Donde ρ es la densidad del fluido, A es el área de sección transversal del objeto y Cd es el coeficiente de resistencia aerodinámica.
El producto ½ ρ.A.Cd es una constante aerodinámica llamada D, cuyas unidades SI son kg/m, por lo tanto:
Froce = Dv2
Este modelo es más apropiado cuando la velocidad de los objetos es media o alta, ya que el movimiento produce turbulencia o remolinos a su paso en el fluido.
Una pelota de tenis en movimiento y los autos en la autopista son ejemplos de objetos en los cuales este modelo funciona bastante bien.
La fuerza viscosa surge debido a que el sólido debe apartar las capas de fluido para poder moverse a través de él. La existencia de varios modelos se debe a que esta fuerza depende de múltiples factores, tales como la viscosidad del fluido, la velocidad y forma del objeto.
Hay objetos más aerodinámicos que otros y muchos se diseñan justamente para que la resistencia del medio reduzca al mínimo su velocidad.
Índice del artículo
Cualquier persona u objeto que se mueva en un fluido necesariamente experimenta resistencia proveniente del medio, pero muchas veces se desprecian estos efectos para aplicaciones sencillas como la caída libre.
En los enunciados de casi todos los problemas de caída libre se advierte que los efectos de la resistencia del aire se desprecian. Esto es porque el aire es un fluido bastante “delgado” y por eso esperamos que el rozamiento que ofrece no sea significativo.
Pero hay otros movimientos en los cuales el roce viscoso tiene una influencia más decisiva, veamos algunos ejemplos:
-Una roca que se deja caer verticalmente en un tubo lleno de aceite experimenta una fuerza que se opone a su descenso, gracias a la resistencia del fluido.
-Los granos de polen son muy pequeños, así que para ellos la resistencia del aire no es despreciable, porque gracias a esta fuerza es que logran mantenerse a flote durante mucho tiempo, causando alergias estacionales.

-En el caso de los nadadores, estos usan gorro y se afeitan completamente para que la resistencia del agua no les reste velocidad.
-Al igual que los nadadores, los ciclistas en contrarreloj experimentan la resistencia del aire, en consecuencia los cascos tienen diseños aerodinámicos para mejorar la eficiencia.
Asimismo la posición del ciclista dentro de un grupo en competencia es relevante. El que encabeza la marcha evidentemente recibe la mayor resistencia del aire, mientras que para los que cierran la marcha, esta es casi nula.
-Una vez que un paracaidista abre el paracaídas, está expuesto al rozamiento viscoso del aire, siendo el modelo más apropiado el que tiene el cuadrado de la velocidad. De esta manera reduce su velocidad y como el roce se opone a la caída, aquella alcanza un valor límite constante.
-Para los automóviles, el coeficiente de resistencia aerodinámica, una constante que se determina experimentalmente y la superficie que presenta contra el viento, son los factores determinantes para reducir la resistencia del aire y reducir el consumo. Por eso se diseñan con los parabrisas inclinados.
-En el experimento de la gota de aceite de Millikan, el físico Robert Millikan estudió el movimiento de gotas de aceite en medio de un campo eléctrico uniforme, llegando a la conclusión de que cualquier carga eléctrica es múltiplo de la carga del electrón.
Para ello era preciso conocer el radio de las gotas, la cual no se podía determinar por medida directa, dado su pequeño tamaño. Pero en este caso el roce viscoso era significativo y las gotas terminaban por ser frenadas. Este hecho permitió determinar el radio de las gotas y posteriormente su carga eléctrica.
En la ecuación para la fuerza de roce viscoso a baja velocidad:
Froce = γv
a) ¿Qué dimensiones debe tener el coeficiente de roce viscoso γ?
b) ¿Cuáles son las unidades de γ en el Sistema Internacional de Unidades?
Solución a
A diferencia de los coeficientes de roce estático o de roce cinético, el coeficiente de fricción viscosa tiene dimensiones, las cuales deben ser de:
Fuerza / velocidad
La fuerza tiene dimensiones de masa x longitud /tiempo2, mientras que las de la velocidad son longitud/tiempo. Al denotarlas de la siguiente manera:
-Masa: M
-Longitud: L
-Tiempo: T
Las dimensiones del coeficiente de roce viscoso γ son:
[M.L /T2] / [L/T] = [M.L.T / L.T2] = M/T
Solución b
En el SI, las unidades de γ son kg/s
Tomando en cuenta la resistencia que opone el agua, encontrar una expresión para la rapidez terminal de una esferita metálica que se deja caer verticalmente en un tubo lleno de aceite, en los casos:
a) Baja velocidad
b) Alta velocidad
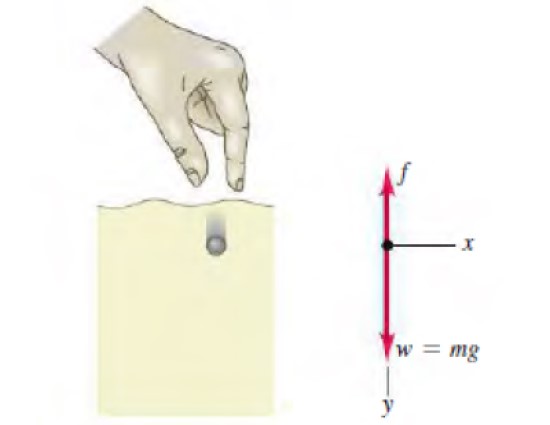
Solución a
En la figura aparece el diagrama de cuerpo libre, mostrando las dos fuerzas que actúan sobre la esferita: el peso hacia abajo y la resistencia del fluido, proporcional a la velocidad, hacia arriba. La segunda ley de Newton para este movimiento establece lo siguiente:
γvt – mg = 0
Donde vt es la rapidez terminal, dada por:
vt = mg / γ
Solución b
Si suponemos velocidades medias a altas, el modelo adecuado es el que tiene la velocidad al cuadrado:
Froce = ½ ρ.A.Cd.v2
Entonces:
½ ρ.A.Cd.v2 – mg = 0
D.v2 – mg = 0
v = √ [mg / D]
En ambas situaciones se tiene que cuanto mayor sea la masa del objeto, mayor es su velocidad terminal.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill
- Universidad de Sevilla. Fuerzas de rozamiento. Recuperado de: laplace.us.es.
