Principio de Pascal: historia, aplicaciones, ejemplos
El principio de Pascal, o ley de Pascal, establece que un cambio en la presión de un fluido confinado en cualquiera de sus puntos es transmitido sin alteración a todos los demás puntos dentro del fluido.
Este principio fue descubierto por el científico francés Blaise Pascal (1623 – 1662). Debido a la trascendencia de los aportes hechos por Pascal a la ciencia, se ha nombrado en su honor la unidad de presión en el Sistema Internacional.
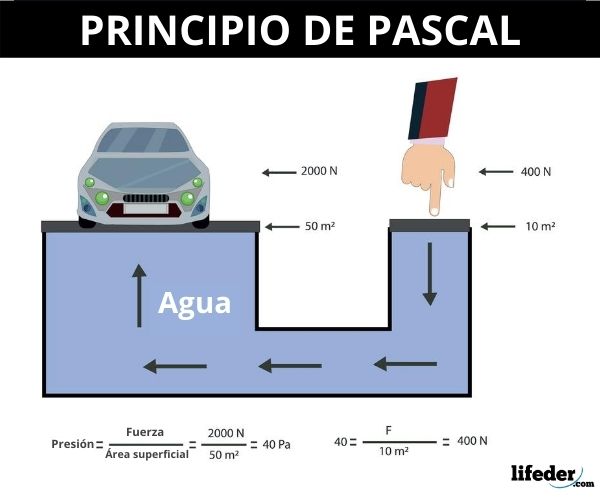
Puesto que la presión se define como el cociente entre la fuerza perpendicular a una superficie entre su área, 1 Pascal (Pa) equivale a 1 newton / m2.
Índice del artículo
- 1 Historia
- 2 Explicación del principio de Pascal
- 3 Aplicaciones
- 4 Ejemplos
- 5 Ejercicio resuelto
- 6 Referencias
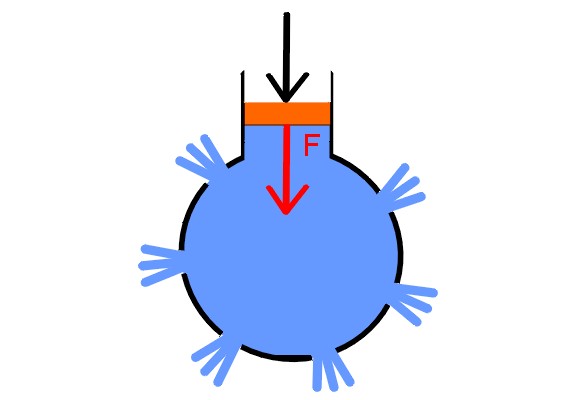
Para comprobar su principio, Pascal ideó una demostración bastante contundente. Tomó una esfera hueca y horadada en varios sitios, puso tapones en todos los agujeros menos en uno, por el cual la llenó de agua. En este colocó una jeringa provista de un émbolo.
Al aumentar suficientemente la presión en el émbolo, los tapones salen disparados al mismo tiempo, porque la presión se transmite por igual a todos los puntos del fluido y en todas las direcciones, demostrando así la ley de Pascal.
Blaise Pascal tuvo una vida corta, marcada por la enfermedad. El increíble alcance de su mente lo llevó a indagar en diversos aspectos de la naturaleza y la filosofía. Sus aportes no se limitaron a estudiar el comportamiento de los fluidos, Pascal también fue pionero de la computación.
Y es que a los 19 años, Pascal creó una calculadora mecánica para que su padre la utilizara en su trabajo en el sistema de impuestos de Francia: la pascalina.
También, junto con su amigo y colega el gran matemático Pierre de Fermat, dieron forma a la teoría de las probabilidades, indispensable en Física y en Estadística. Pascal falleció en París, a la edad de 39 años.
El siguiente experimento es bastante simple: se llena un tubo en U con agua y se le colocan tapones en cada extremo que puedan deslizarse suave y fácilmente, a modo de pistones. Se hace presión contra el pistón izquierdo hundiéndolo un poco y se observa que el de la derecha sube, empujado por el fluido (figura inferior).
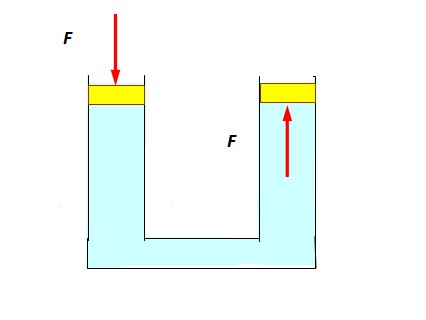
Esto sucede porque la presión se transmite sin disminución alguna a todo punto del fluido, incluyendo los que están en contacto con el pistón de la derecha.
Líquidos como agua o aceite son incompresibles pero a la vez las moléculas tienen suficiente libertad de movimiento, lo cual hace posible que la presión se distribuya sobre el pistón derecho.
Gracias a ello, el pistón derecho recibe una fuerza que es exactamente igual en magnitud y dirección a la que se aplicó a la izquierda, pero de sentido opuesto.
La presión en un fluido estático es independiente de la forma del recipiente. Se demostrará enseguida que la presión varía linealmente con la profundidad y el principio de Pascal es consecuencia de ello.
Una alteración de la presión en cualquier punto, hace que la presión en otro punto se altere en la misma cantidad. De lo contrario existiría una presión extra que haría fluir el líquido.
Un fluido en reposo ejerce una fuerza sobre las paredes del recipiente que lo contiene e igualmente sobre la superficie de cualquier objeto sumergido en él. En el experimento de la jeringa de Pascal se ve que los chorritos de agua salen perpendicularmente a la esfera.
Los fluidos reparten la fuerza perpendicularmente en la superficie sobre la que actúa, por eso es conveniente introducir el concepto de presión media Pm como la fuerza perpendicular ejercida F⊥ por área A, cuya unidad SI es el pascal:
Pm = F⊥ / A
La presión aumenta con la profundidad. Se puede ver aislando una pequeña porción de fluido en equilibrio estático y aplicando la segunda ley de Newton:

Las fuerzas horizontales se cancelan por pares, pero en la dirección vertical las fuerzas se agrupan así:
∑Fy = F2 – F1 – mg = 0 → F2 – F1 = mg
Expresando la masa en términos de la densidad ρ= masa /volumen:
P2.A- P1.A = ρ x volumen x g
El volumen de la porción de fluido es el producto A x h:
A.(P2 – P1) = ρ x A x h x g
ΔP = ρ.g.h Teorema fundamental de la hidrostática

El principio de Pascal se ha utilizado para construir numerosos dispositivos que multiplican la fuerza y facilitan labores como levantar pesos, estampar sobre metal o prensar objetos. Entre ellos se destacan:
-La prensa hidráulica
-El sistema de frenos de los automóviles
-Palas mecánicas y brazos mecánicos
-El gato hidráulico
-Grúas y ascensores
A continuación, veamos cómo el principio de Pascal hace que las fuerzas pequeñas se transformen en fuerzas grandes para realizar todos estos trabajos. La prensa hidráulica es el ejemplo más característico y será analizado a continuación.

Para construir una prensa hidráulica se toma el mismo dispositivo de la figura superior, es decir un recipiente en forma de U, del cual ya sabemos que de un pistón al otro se transmite la misma fuerza. La diferencia será el tamaño de los pistones y esto es lo que hace funcionar al dispositivo.
La siguiente figura muestra el principio de Pascal en acción. La presión es la misma en todos los puntos del fluido, tanto en el pistón pequeño como en el grande:
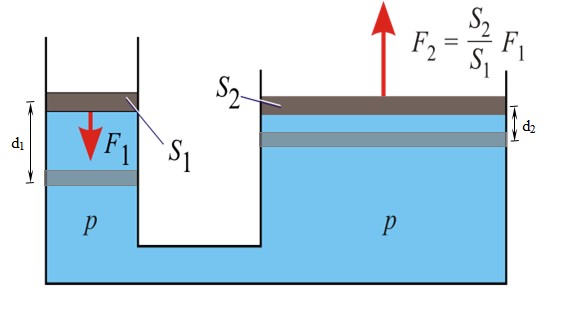
p = F1 / S1 = F2 / S2
La magnitud de la fuerza que se transmite al pistón grande es:
F2 = (S2 / S1). F1
Como S2 > S1, resulta en F2 > F1, por lo tanto la fuerza de salida se ha multiplicado en el factor dado por el cociente entre las áreas.
En esta sección se presentan ejemplos de aplicación.
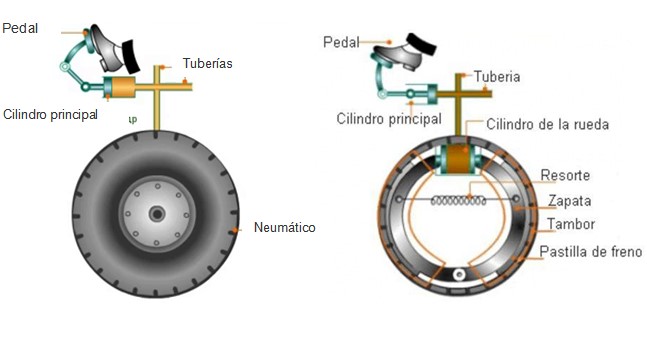
Los frenos de los automóviles hacen uso del principio de Pascal a través de un fluido hidráulico que llena unos tubos conectados a las ruedas. Cuando necesita detenerse, el conductor aplica una fuerza oprimiendo el pedal del freno y generando una presión en el fluido.
Por el otro extremo, la presión empuja las pastillas de freno contra el tambor o los discos de freno que giran en conjunto con las ruedas (no con los neumáticos). El rozamiento resultante hace que el disco se vaya deteniendo, ralentizando también a las ruedas.
En la prensa hidráulica de la figura inferior, el trabajo de entrada debe ser igual al trabajo de salida siempre y cuando no se tome en cuenta la fricción.

La fuerza de entrada F1 hace que el pistón recorra una distancia d1 al bajar, mientras la fuerza de salida F2 permite un recorrido d2 del pistón que sube. Si el trabajo mecánico realizado por ambas fuerzas es el mismo:
F1.d1 = F2. d2
La ventaja mecánica M es el cociente entre las magnitudes de la fuerza entrada y la de salida:
M = F2/F1 = d1/d2
Y como se demostró en la sección precedente, también se puede expresar como el cociente entre las áreas:
F2/F1 = S2 / S1
Pareciera que se logra hacer trabajo gratis pero en verdad no se está creando energía con este dispositivo, ya que la ventaja mecánica se obtiene a expensas del desplazamiento del pistón pequeño d1.
Así que para optimizar el rendimiento se agrega al dispositivo un sistema de válvulas de tal manera que el pistón de salida vaya elevándose gracias a impulsos breves sobre el pistón de entrada.
De esta forma el operario de un gato hidráulico de garaje bombea varias veces para ir levantando poco a poco un vehículo.
En la prensa hidráulica de la figura 5, las áreas de los pistones son 0.5 pulgadas cuadradas (pistón pequeño) y 25 pulgadas cuadradas (pistón grande). Encuentre:
a) La ventaja mecánica de esta prensa.
b) La fuerza necesaria para levantar una carga de 1 tonelada.
c) La distancia en la que debe actuar la fuerza de entrada para levantar dicha carga en 1 pulgada.
Expresar todos los resultados en unidades del sistema británico y del Sistema Internacional SI.
Solución
a) La ventaja mecánica es:
M = F2/F1 = S2/S1 = 25 in2 / 0.5 in2 = 50
b) 1 tonelada equivale a 2000 lb-fuerza. La fuerza necesaria es F1:
F1 = F2 / M = 2000 lb-fuerza / 50 = 40 lb- fuerza
Para expresar el resultado en el Sistema Internacional se requiere del siguiente factor de conversión:
1 lb-fuerza = 4.448 N
Por lo tanto la magnitud de F1 es 177.92 N.
c) M = d1/d2 → d1 = M.d2 = 50 x 1 in = 50 in
El factor de conversión necesario es: 1 in = 2.54 cm
d1 = 127 cm = 1.27 m
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 417-450.
- College Physics. Pascal’s principie. Recobrado de: opentextbc.ca.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 4. Fluidos y Termodinámica. Editado por Douglas Figueroa (USB). 4 – 12.
- Rex, A. 2011. Fundamentos de Física. Pearson. 246-255.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.301-320.
